1. 双击appuploader.exe 启动appuploader
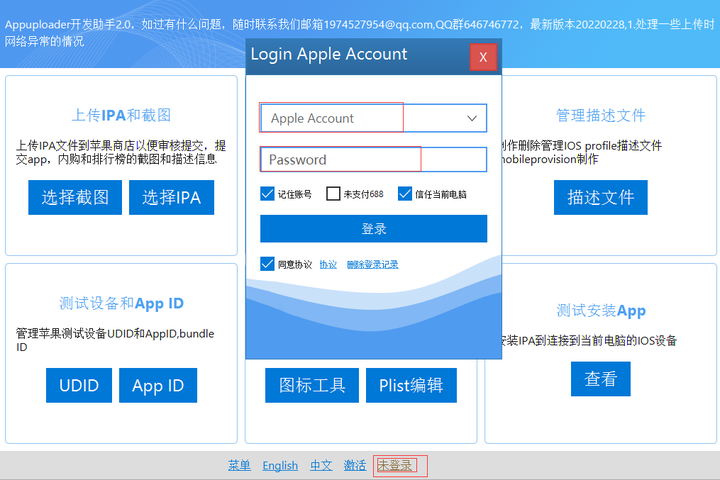
  2. 点击底部的未登录，弹出登录框
  3. 在登录框内输入apple开发者账号
  4. 如果没有apple开发者账号，只是普通的apple账号，请勾选上未支付688
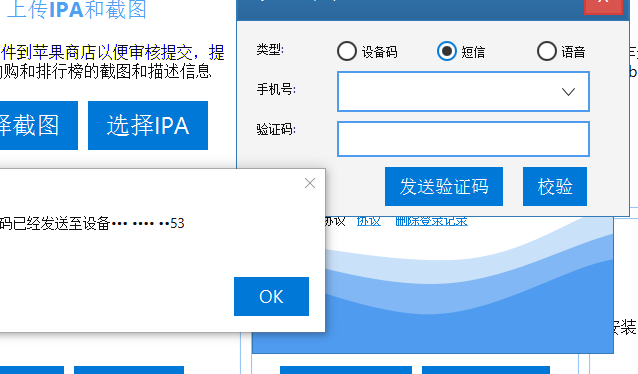
  5. 然后软件会提示输入验证码，点击验证，验证成功就可以使用各项功能了 最新版本已经优化了未支付688给apple的账号的登录流程，无需再安装其他软件，可以直接下载最新版本

​
编辑切换为居中
添加图片注释，不超过 140 字（可选）
 
 
为了安全，账号必须开启验证码验证功能，才能使用appuploader，启用验证码功能请前往 https://appleid.apple.com ,在账号管理里面可以设置密保手机。
验证码输入界面留意是短信还是设备码，如果是收到了短信则选择短信，如果是设备码则选择设备码。
每天验证码数量是有限制的，如果不断发送，账号会被限制登录，所以不要快速不断的点击发送。如果提示验证码发送次数过多，则需要等待第二天再试了。
 

​
编辑切换为居中
添加图片注释，不超过 140 字（可选）
 
 
如果您只有上传权限，没有账号的其他权限，也没有账号的密码，可以通过上传专用密码登录。 打开软件后点击 选择ipa 或者选择截图 按钮，会弹出直接输入上传专用密码登录功能，此方法登录后只能上传ipa和截图，无法进行其他的证书管理之类的功能。并且此方法登录后，账号和上传密码不会被记住，每次打开软件都需要重新输入。
 
没支付费用给apple的账号，或者过期的账号，没有正常的开发者权限，只有非常有限的开发测试权限功能。 限制比较多，例如无法进行上传上架，无法创建发布证书，app无法使用推送功能，测试设备最多3个，有效期最多7天等等。但是进行普通的开发和安装到自己手机进行测试还是可以的。
登录的时候需要，勾选未支付688选项，登录进去后，管理证书的时候也只有开发证书一种类型。免费账号，在登录appuploader之前，需要下载icloud，并且登录icloud，确保账号是ok的 。 icloud下载地址：https://support.apple.com/zh-cn/HT204283 下载icloud 。安装icloud，并且下载apple官网版本，不要从windows store下载 ,您可以从 Apple 网站下载 Windows 版 iCloud。
 

​
编辑切换为居中
添加图片注释，不超过 140 字（可选）
 

appuploader 常规使用登录方法的更多相关文章

  1. ECSHOP手机号码或邮箱用户名都可以登录方法

    ECSHOP手机号码或邮箱用户名都可以登录方法 ECSHOP教程/ ecshop教程网(www.ecshop119.com) 2013-06-30   有不少人都在找支持ECShop用户名.邮箱或手号 ...

  2. SharePoint2010 自定义代码登录方法

    转:http://yysyb123.blog.163.com/blog/static/192050472011382421717/ SharePoint2010 自定义代码登录方法 (自定义Form验 ...

  3. 华为S5700交换机初始化和配置SSH和TELNET远程登录方法

    基础设置: 配置登陆IP地址<Quidway> system-view                                                            ...

  4. Linux—禁止用户SSH登录方法总结

    Linux-禁止用户SSH登录方法总结 一.禁止用户登录 1.修改用户配置文件/etc/shadow       将第二栏设置为"*",如下.那么该用户就无法登录.但是使用这种方式 ...

  5. Linux SSH安全策略限制IP登录方法(转)

    本文介绍了Linux SSH安全策略限制IP登录的两种方法.具体如下: 方法一: 首先需要限制登录的ip(或者如果需要自己本地登录,查看最后登录ip即可) Vim /etc/hosts.allow 输 ...

  6. Spring Security入门（2-3）Spring Security 的运行原理 4 - 自定义登录方法和页面

    参考链接,多谢作者: http://blog.csdn.net/lee353086/article/details/52586916 http元素下的form-login元素是用来定义表单登录信息的. ...

  7. 图解SSH原理及两种登录方法

    SSH(Secure Shell)是一套协议标准,可以用来实现两台机器之间的安全登录以及安全的数据传送,其保证数据安全的原理是非对称加密. 传统的对称加密使用的是一套秘钥,数据的加密以及解密用的都是这 ...

  8. ssh免密登录方法不生效？Authentication refused: bad ownership or modes for directory

    机器A通过ssh登录机器B,方法有两种: 1.密码方式 2.密钥方式: 两种方式同时开启的时候,优先使用密钥方式. 密钥登录方式的配置方法是,首先在登录机器B上创建文件authorized_keys( ...

  9. taotao单点登录的用户Controller、service（注册、登录、验证是否登录方法）

    接口文档: 1.1. 注册接口 1.1.1. 检查数据是否可用 请求方法 GET URL http://sso.taotao.com/user/check/{param}/{type} 参数说明 格式 ...

  10. win7用户账户自动登录方法

    为了计算机安全,相信使用Windows7系统的朋友大多都为自己的用户账户设置了或简单或复杂的密码,其实对于个人电脑来说,开机登录输入密码有时候会显得累赘,毕竟用户账户密码不仅仅是为了防止他人登录. 那 ...

随机推荐

  1. Acwing周赛102

    倍增 这是一道简单数论题 using namespace std; typedef long long LL; const int N = 1e5 + 10; int a[N], n; int div ...

  2. 【腾讯云 HAI域探秘】探索AI绘画之路：利用腾讯云HAI服务打造智能画家

    前言 随着人工智能的飞速发展,AI在艺术创作领域的应用正经历着一场革命性的变革.在这个数字时代,腾讯云的高性能应用服务HAI(Hyper Application Inventor)为艺术家和创作者提供 ...

  3. java固定窗口大小

    this.setResizable(false);//////frame.setResizable(false)

  4. AtCoder Beginner Contest 240 F - Sum Sum Max

    原题链接F - Sum Sum Max 首先令\(z_i = \sum\limits_{k = 1}^i y_k\),\(z_0 = 0\),\(z_i\)就是第\(i\)段相同的个数的前缀和. 对于 ...

  5. 神经网络入门篇：神经网络的梯度下降（Gradient descent for neural networks）

    神经网络的梯度下降 在这篇博客中,讲的是实现反向传播或者说梯度下降算法的方程组 单隐层神经网络会有\(W^{[1]}\),\(b^{[1]}\),\(W^{[2]}\),\(b^{[2]}\)这些参数 ...

  6. React、Umi、RN 整体理解

    可以少去理解一些不必要的概念,而多去思考为什么会有这样的东西,它解决了什么问题,或者它的运行机制是什么? React 1. React 起源和发展(是什么?) React 是用于构建用户界面的 Jav ...

  7. Python 哈希表的实现——字典

    哈喽大家好,我是咸鱼 接触过 Python 的小伙伴应该对[字典]这一数据类型都了解吧 虽然 Python 没有显式名称为"哈希表"的内置数据结构,但是字典是哈希表实现的数据结构 ...

  8. JAVA学习week2

    这周:根据老师在群里面推荐的JAV学习路线,初步规划了一下学习方案 并找到了相关的视频,目前来说在学习SE.学习内容:环境变量的配置和简单的hello world程序书写的注意点 下周:打算进行简单的 ...

  9. 【uniapp】【外包杯】学习笔记day04 | 学习模板+vue相关知识+环境搭建

    没啥好说的,人与人的悲欢并不相同,我只觉得吵闹. 好烦啊,虽然不应该总说一些低气压的话,不过目前预见的就是有很多工作要做,并且对于完成的希望也有点没有,就这样吧,没啥好说的. 昨天做了python的作 ...

  10. Miller_Rabin 学习笔记

    费马小定理:对于任意一个质数满足:\(a^{p-1}\equiv1\pmod p\) 二次探测:对于任意一个奇质数满足:\(x^2\equiv1\pmod p\) 的解为 \(x=1\) 或 \(x= ...