AutoCad .Net二次开发求两曲线最小距离

测试结果：

主要思路：假设有两条曲线分别是c1和c2，把c1按照1的距离划分我这里用变量jd表示，得到一个曲线集合coll，然后遍历coll，得到coll中每一个曲线的两个端点，再用这两个端点分别求离曲线c2的最短距离，直接使用开发库的GetClosestPointTo方法就可以了，直到遍历完整个coll集合就能得到最短距离和其对应的点。

主要代码得到曲线集合coll：

 public List<Curve> GetCurves(Curve curve ,double jd)
        {
            List<Curve> lstCurves = new List<Curve>();

            double totalLength = curve.GetDistanceAtParameter(curve.EndParam);

            if (totalLength < jd)
            {
                lstCurves.Add(curve);
                return lstCurves;
            }
            double addLength = ;

            Point3dCollection pt3dCol = new Point3dCollection();

            while (addLength < totalLength)
            {
                pt3dCol.Add(curve.GetPointAtDist(addLength));
                addLength += jd;

            }
            if (addLength != totalLength)
                pt3dCol.Add(curve.GetPointAtDist(totalLength));

           DBObjectCollection dbObjColl= curve.GetSplitCurves(pt3dCol);

            foreach (var item in dbObjColl)
            {
                lstCurves.Add((Curve)item);
            }

            dbObjColl.Dispose();

            return lstCurves;
        }

主要代码得到最短距离和最近点：

public Line GetMinLine(Curve curve1,Curve curve2,double jd)
        {
            List<Curve> lstCurves = GetCurves(curve1, jd);

            double minVal = double.MaxValue;
            Point3d ptMin1 = Point3d.Origin;
            Point3d ptMin2 = Point3d.Origin;
            foreach (var c in lstCurves)
            {
                Point3d pt1 = c.StartPoint;
                Point3d pt2 = c.EndPoint;

                var pt11=curve2.GetClosestPointTo(pt1, false);
                var pt22= curve2.GetClosestPointTo(pt2, false);

                var l1 = pt11.DistanceTo(pt1);
                var l2 = pt22.DistanceTo(pt2);

                if (l1 < minVal)
                {
                    minVal = l1;
                    ptMin1 = pt11;
                    ptMin2 = pt1;
                }
                if (l2 < minVal)
                {
                    minVal = l2;
                    ptMin1 = pt22;
                    ptMin2 = pt2;
                }

            }
            ed.WriteMessage("\n最短距离：" + minVal + "\n");

            return new Line(ptMin1,ptMin2);
        }

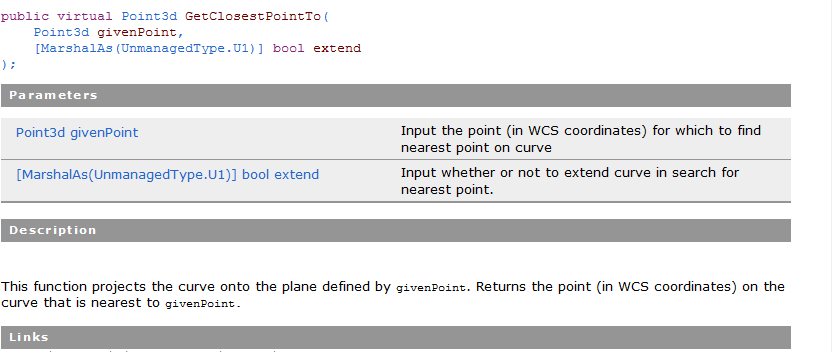
关于GetClosestPointTo介绍如下：