先说最暴力的算法，直接对一万内的每个数字暴力分解因子(对每个数字的时间复杂度是O(sqrt(n)的)，然后，用个数组记录下来因子和，然后寻找 亲密数。
好一点：要先打个素数表，然后对每个数字，分解素因子，
假设因子和函数为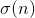，则, 推导后： ------>证明过程见《初等数论及其应用》(原书第六版)184-185页
有个坑就是a!=b,在这里错了好几发。。。。
看了下官方的题解，最终用的方法就是我图片里的那个公式。
------------->开启了支持数学公式，可是还是不支持，很蛋疼，所以传了图片

Project Euler Problem 21-Amicable numbers的更多相关文章

  1. Project Euler 42 Coded triangle numbers

    题意:三角形数序列的第n项由公式tn = 1/2n(n+1)给出:因此前十个三角形数是: 1, 3, 6, 10, 15, 21, 28, 36, 45, 55, - 将一个单词的每个字母分别转化为其 ...

  2. Project Euler Problem (1~10)

    1.If we list all the natural numbers below 10 that are multiples of 3 or 5, we get 3, 5, 6 and 9. Th ...

  3. Project Euler 88：Product-sum numbers 积和数

    Product-sum numbers A natural number, N, that can be written as the sum and product of a given set o ...

  4. Project Euler Problem 10

    Summation of primes Problem 10 The sum of the primes below 10 is 2 + 3 + 5 + 7 = 17. Find the sum of ...

  5. Project Euler 2 Even Fibonacci numbers

    题意:斐波那契数列中的每一项都是前两项的和.由1和2开始生成的斐波那契数列前10项为:1, 2, 3, 5, 8, 13, 21, 34, 55, 89, -考虑该斐波那契数列中不超过四百万的项,求其 ...

  6. Project Euler Problem 5-Smallest multiple

    对每个数字分解素因子,最后对每个素因子去其最大的指数,然后把不同素因子的最大指数次幂相乘,得到的就是最小公倍数 python不熟练,代码比较挫 mp = {} def process(n): i = ...

  7. Project Euler problem 62

    题目的大意很简单 做法的话. 我们就枚举1~10000的数的立方, 然后把这个立方中的有序重新排列,生成一个字符串s, 然后对于那些符合题目要求的肯定是生成同一个字符串的. 然后就可以用map来搞了 ...

  8. Project Euler problem 63

    这题略水啊 首先观察一下. 10 ^ x次方肯定是x + 1位的 所以底数肯定小于10的 那么我们就枚举1~9为底数 然后枚举幂级数就行了,直至不满足题目中的条件即可break cnt = 0 for ...

  9. Project Euler problem 61

    题意很明了. 然后我大概的做法就是暴搜了 先把每个几边形数中四位数的处理出来. 然后我就DFS回溯着找就行了. 比较简单吧. #include <cstdio> #include < ...

随机推荐

  1. dedecms list标签调用附加表字段--绝对成功

    使用list标签调用附加表字段的时候会忽略一个地方,明明附加字段名已经添加进去了就是调用不出来 经过在网上查询了资料,说的天花乱坠,也都实践过一些,但是就是不成功鞋面介绍一下犯的低级错误在哪里 {de ...

  2. Leetcode669.Trim a Binary Search Tree修建二叉树

    给定一个二叉搜索树,同时给定最小边界L 和最大边界 R.通过修剪二叉搜索树,使得所有节点的值在[L, R]中 (R>=L) .你可能需要改变树的根节点,所以结果应当返回修剪好的二叉搜索树的新的根 ...

  3. input只能输入数字和小数点，并且只能保留小数点后两位 - CSDN博客

    1.给文本框添加一个onkeyup=’clearNoNum(this)’点击事件 2.建立clearNoNum方法 function clearNoNum(obj) { obj.value = obj ...

  4. LUOGU P2587 [ZJOI2008]泡泡堂

    传送门 解题思路 刚开始先写了个田忌赛马的贪心,就是要是打不过就拿最弱的送死,30分...后来瞄了眼题解,发现这样是错的,比如说这样的数据 : 3 3 2 3 1 如果用田忌赛马的话,让2-3 3-1 ...

  5. iPhone使用CoreTelephony获得SIM卡网络运营商资讯和通话资料

    注意要加头文件目录 /System/Library/Frameworks/CoreTelephony.framework/Headers 到 build 设置 Header Search Paths, ...

  6. js数组求交集

    求两个数组的交集 var arr1 = [1,2,3]; var arr2 = [2,3,4]; var arr3; arr3 = arr1.filter(function(num) { return ...

  7. vue中router以及route的使用

    路由基本概念 route,它是一条路由. { path: '/home', component: Home } routes,是一组路由. const routes = [ { path: '/hom ...

  8. Leetcode704.Binary Search二分查找

    给定一个 n 个元素有序的(升序)整型数组 nums 和一个目标值 target  ,写一个函数搜索 nums 中的 target,如果目标值存在返回下标,否则返回 -1. 示例 1: 输入: num ...

  9. PHP学习（函数）

    可变函数,即通过变量的值来调用函数,因为变量的值是可变的,所以可以通过改变一个变量的值来实现调用不同的函数. 经常会用在回调函数.函数列表,或者根据动态参数来调用不同的函数.可变函数的调用方法为变量名 ...

  10. [转] javascript核心

    原文:http://dmitrysoshnikov.com/ecmascript/javascript-the-core/ 对象 原型链 构造函数 执行上下文栈 执行上下文 变量对象 活动对象 作用域 ...