清北学堂—2020.1提高储备营—Day 1 afternoon（二分、分治、贪心）

qbxt Day 1 afternoon

——2020.1.17 济南主讲：李佳实

目录一览

1.二分法
2.分治
3.贪心

总知识点：基础算法

一、二分法

（1）算法分析：二分法是一种暴力枚举的优化版，它可以使时间复杂度大大减少，从而达到优化的效果。它同时又是一种典型的分治思想的应用。
（2）本质：把待求解问题分为两部分，每一部分分别求解。
（3）解决问题：具有单调性质的题
（4）时间复杂度：若暴力枚举要O（N），那二分需要O(log N)、
（5）代码框架：

整数版：

---------------------------------------------------------------------------------------------

小数版：

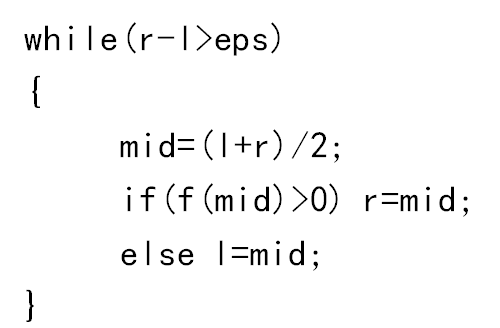
（6）例题：派

分析：首先这个题我们看到就能想出一种最直接的方法——暴力枚举扫一遍。这样做方法显然没问题，但是时间复杂度上不可行，显然会TLE。我们要优化这个方法，使他能卡过去。二分法就是一种很好的方法。我们先枚举扫一遍，再二分，求得正确答案。
代码：

#include<iostream>
#include<cstring>
#include<cstdio>
#include<algorithm>
#define N 1000
#define M 1000
using namespace std;
int n,f,a[N];
bool check(int x){  //寻找答案区间
    int s=0;
    for(int i=1;i<=n;i++) s+=a[i]/x;
    if(s>=f) return true;
    return false;
}
int main(){
    cin>>n>>f;
    f++;
    int sum=0;
    for(int i=1;i<=n;i++){
        cin>>a[i];
        sum+=a[i];
    }
    int l=0,r=sum/f;
    //二分模板求答案
    while(l<r){
        int mid=(l+r+1)/2;
        if(check(mid)) l=mid;
        else r=mid-1;
    }
    cout<<l<<endl;
}

二、分治

1.算法描述：把一个复杂的问题简单化，从全局变成局部，逐渐缩小问题的规模，更加高效的解决问题的一种算法。
2.应用实例：
（1）快速排序：O(nlogn)
步骤：
1.找一个轴值
2.序列重新排列，小于轴值的放在前面，轴值放在中间，大于轴值的放在右边.
3.两边分别递归即可
代码：

inline void quick_sort(int left,int right){
    int i=left,j=right,mid=a[(left+right)/2];
    while(i<=j){
        while(a[i]<mid) i++;
        while(a[j]>mid) j--;
        if(i<=j){
            swap(a[i],a[j]);
            i++,j--;
        }
    }
    if(left<j) quick_sort(left,j);
    if(i<right) quick_sort(i,right);
}

（2）归并排序：O(nlogn)
步骤：
1.把序列等分为两部分，分别递归
2.然后把它们归并起来
代码：

inline void merge_sort(int left,int right){
    if(left==right) return;
    int mid=(left+right)/2,i,j,tmp=1;
    merge_sort(left,mid);
    merge_sort(mid+1,right);
    for(i=1,j=mid+1;i<=mid&&j<=right;){
        if(a[i]>a[j]) c[tmp++]=a[j++];
        else c[tmp++]=a[i++];
    }
    if(i<=mid){
        for(;i<mid;) c[tmp++]=a[i++];
    }
    if(j<=right){
        for(;j<=right;) c[tmp++]=a[j++];
    }
    for(i=left;i<=right;i++) a[i]=c[i];
}

（3）求逆序对
逆序对定义：i<j但a[i]>a[j]
分析：还是老套路，暴力。不过这显然不行，这个时间复杂度很高。当我们在进行Merge_sort（归并排序）时，已经默认组成了多组逆序对。
为什么呢，我来分析一下原因。分治思想：把整个序列分成两部分，我们要的总逆序对数量=左半的+右半的。这两项可以慢慢递归求解，这就完成了大部分。还有最关键的一部——合并。这一步也很简单，随便打下O（N）就能解决。
代码：

注：套了一个Merge——sort的大板子，加了一个ans，来统计逆序对。

　三、贪心

1.算法描述：贪心算法是指在对问题求解时，总是做出在当前看来是最优的决策。即就是不从全局最优方面考虑，只考虑局部最优情况它有时可以得到全局的最优解，这取决于策略。
2.做题技巧：当我们试图用贪心法来解决一道题的时候，最好能先证明贪心的正确性，否则只靠猜测一般来说是不正确的。
3.例题：（极其简单）
（1）排队接水
题目描述
有n个人在一个水龙头前排队接水，假如每个人接水的时间为Ti，请编程找出这n个人排队的一种顺序，使得n个人的平均等待时间最小。
输入格式
输入文件共两行，第一行为n；第二行分别表示第1个人到第n个人每人的接水时间T1，T2，…，Tn，每个数据之间有1个空格。
输出格式
输出文件有两行，第一行为一种排队顺序，即1到n的一种排列；第二行为这种排列方案下的平均等待时间(输出结果精确到小数点后两位)。

分析：这个题一眼看上去就像贪心，你只需要以时间为标准，将数据进行排序，时间小的在前，等待时间就少，然后就解决了。

代码：

#include<stdio.h>
#include<algorithm>
using std::sort;
struct node {
    int n,time;
}p[1002];
double result;
inline bool comp(node a,node b) {
    if(a.time!=b.time) return a.time<b.time;
    return a.n<b.n;
}
int main() {
    int x;
    scanf("%d",&x);
    for(int i=1;i<=x;i++){
        scanf("%d",&p[i].time);
        p[i].n=i;
    }
    sort(p+1,p+x+1,comp);
    for(int i=1;i<=x;i++)  printf("%d ",p[i].n);
    printf("\n");
    for(int i=1;i<=x;i++)  result+=i*p[x-i].time;
    result/=x;
    printf("%.2f",result);
    return 0;
}

-----------------------------------------------THE END----------------------------------------------------