Fix a Tree

Fix a Tree

A tree is an undirected connected graph without cycles.

Let's consider a rooted undirected tree with n vertices, numbered 1 through n. There are many ways to represent such a tree. One way is to create an array with n integers p₁, p₂, ..., p_n, where p_i denotes a parent of vertex i (here, for convenience a root is considered its own parent).

For this rooted tree the array p is [2, 3, 3, 2].

Given a sequence p₁, p₂, ..., p_n, one is able to restore a tree:

1. There must be exactly one index r that p_r = r. A vertex r is a root of the tree.
2. For all other n - 1 vertices i, there is an edge between vertex i and vertex p_i.

A sequence p₁, p₂, ..., p_n is called valid if the described procedure generates some (any) rooted tree. For example, for n = 3 sequences (1,2,2), (2,3,1) and (2,1,3) are not valid.

You are given a sequence a₁, a₂, ..., a_n, not necessarily valid. Your task is to change the minimum number of elements, in order to get a valid sequence. Print the minimum number of changes and an example of a valid sequence after that number of changes. If there are many valid sequences achievable in the minimum number of changes, print any of them.

Input

The first line of the input contains an integer n (2 ≤ n ≤ 200 000) — the number of vertices in the tree.

The second line contains n integers a₁, a₂, ..., a_n (1 ≤ a_i ≤ n).

Output

In the first line print the minimum number of elements to change, in order to get a valid sequence.

In the second line, print any valid sequence possible to get from (a₁, a₂, ..., a_n) in the minimum number of changes. If there are many such sequences, any of them will be accepted.

Examples

Input

4
2 3 3 4

Output

1
2 3 4 4 

Input

5
3 2 2 5 3

Output

0
3 2 2 5 3 

Input

8
2 3 5 4 1 6 6 7

Output

2
2 3 7 8 1 6 6 7

Note

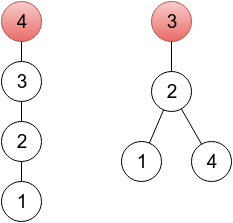
In the first sample, it's enough to change one element. In the provided output, a sequence represents a tree rooted in a vertex 4 (because p₄ = 4), which you can see on the left drawing below. One of other correct solutions would be a sequence 2 3 3 2, representing a tree rooted in vertex 3 (right drawing below). On both drawings, roots are painted red.

In the second sample, the given sequence is already valid.

分析：dfs循环一遍，遇到环时该点是可能修改的答案。注意，如果树已有根的话就用任意一个根，否则在断点处建一个根；

代码：

#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <cmath>
#include <algorithm>
#include <climits>
#include <cstring>
#include <string>
#include <set>
#include <map>
#include <queue>
#include <stack>
#include <vector>
#include <list>
#include <ext/rope>
#define rep(i,m,n) for(i=m;i<=n;i++)
#define rsp(it,s) for(set<int>::iterator it=s.begin();it!=s.end();it++)
#define vi vector<int>
#define pii pair<int,int>
#define mod 1000000007
#define inf 0x3f3f3f3f
#define pb push_back
#define mp make_pair
#define fi first
#define se second
#define ll long long
#define pi acos(-1.0)
const int maxn=2e5+;
const int dis[][]={{,},{-,},{,-},{,}};
using namespace std;
using namespace __gnu_cxx;
ll gcd(ll p,ll q){return q==?p:gcd(q,p%q);}
ll qpow(ll p,ll q){ll f=;while(q){if(q&)f=f*p;p=p*p;q>>=;}return f;}
int n,m,a[maxn],vis[maxn],cnt,ans;
bool flag;
set<int>p;
void dfs(int now)
{
    vis[now]=cnt;
    if(vis[a[now]]==cnt)
    {
        p.insert(now);return;
    }
    else if(vis[a[now]])return;
    else dfs(a[now]);
}
int main()
{
    int i,j,k,t;
    scanf("%d",&n);
    rep(i,,n){
        scanf("%d",&a[i]);
        if(a[i]==i)
            ans=i,flag=true;
    }
    rep(i,,n)
        if(!vis[i])++cnt,dfs(i);
    if(flag==false)
        printf("%d\n",p.size()),ans=*p.begin();
    else
        printf("%d\n",p.size()-);
    rep(i,,n)
    {
        if(p.find(i)!=p.end())a[i]=ans;
    }
    rep(i,,n)
        printf("%d ",a[i]);
    //system ("pause");
    return ;
}