javascript中的三角学

　　　三角学主要研究三角形和它们的边角关系，包含一个90度角的三角形被称为直角三角形。在这里主要研究直角三角形相关的知识。

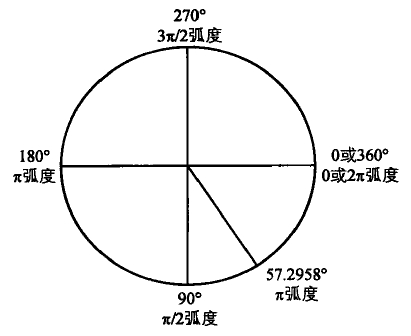
　　　1. 角度和弧度

　　　360(角度) = 2*Math.PI(弧度)　

degrees = radians * 180/Math.PI
角度等于弧度乘于180再除于PI

radians = degrees * Math.PI/180
弧度等于角度度乘于PI再除于180

　　　 

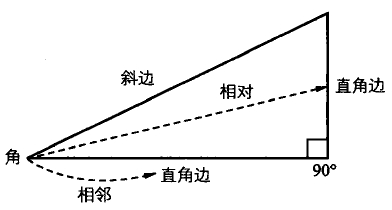
　　　2. 三角形的边

　　　在一个直角三角形中，与90度角相邻的两条边称为直角边，与它对应的边称为斜边，斜边总是最长的边。

　　　

　　　3. 三角函数

　　  正弦：一个角的对边与斜边的比例。

　　　

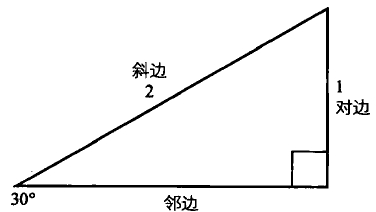
　　　一个30度角的正弦值　　

Math.sin(30 * Math.PI / 180)

　　　

　　　余弦：一个角的邻边与斜边的比例。

　　　

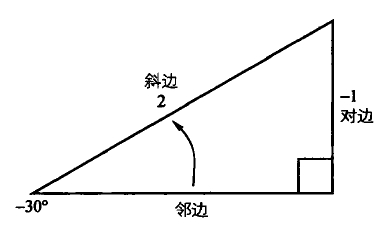
　　　一个30度角的余弦值

Math.cos(30 * Math.PI / 180)

　　　正切：一个角的对边与邻边的比例。

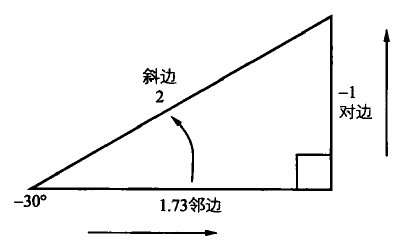
　　　一个30度角的正切值

Math.tan(30 * Math.PI / 180)

　　　反正弦：Math.asin(ratio)

　　　反余弦：Math.acos(ratio)　　　

　　　反正弦和反余弦是正弦和余弦的逆运算，输入一个比率，获得一个对应角的弧度。　

Math.sin(30 * Math.PI / 180) //约为0.5
 Math.asin(0.5) * 180 / Math.PI //约为30度

　　　反正切：Math.atan(ratio)

　　　反正切通过一个角的对边与邻边比率得到角的弧度。

Math.tan(30 * Math.PI / 180) //约为0.578
 Math.atan(0.578) * 180 / Math.PI //约为30度

　　 　javascript中另一个反正切：Math.atan2(y,x)　　

　　　

　　　　javascript中坐标系统和平常的不一样。

　　　　

　　　

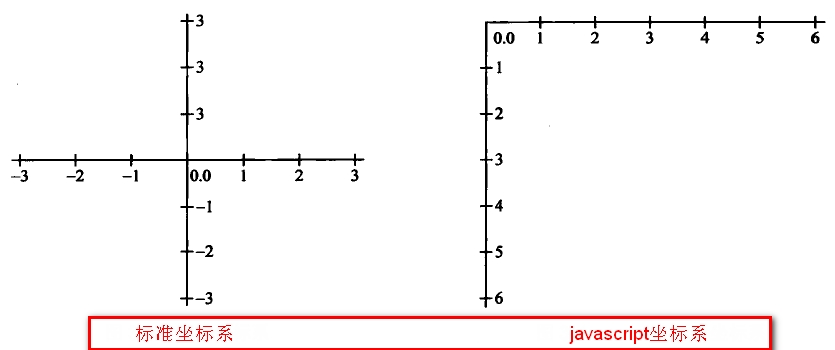
　　　  在javascript坐标系中通过反正切(Math.atan2)计算一个变化点对应一个固定点的角度：

　　　　固定点(arrow.x, arrow.y )

　　　　变化点(mouse.x, mouse.y)

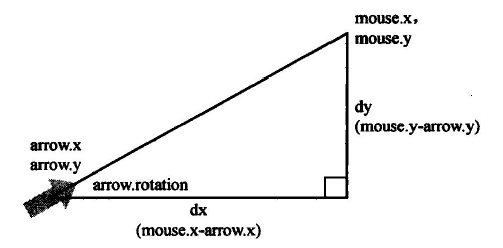
var dx = mouse.x - arrow.x,
    dy = mouse.y - arrow.y,
    angle = Math.atan2(dy, dx);
console.log('角度为：' + angle );

　　 在javascript计算中，Math.atan2(y, x) 能正确的计算出对应角。

　　　4. 勾股定理

　　　直角三角形中，两条直角边的平方和等于斜边的平方。

　　　

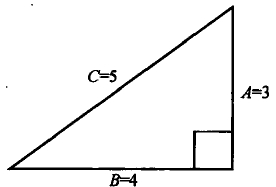
　　　A的平方 + B的平方 = C的平方

　　　计算两点之间的距离

　　　点1：(x1, y1)

　　　点2：(x2, y2)

var dx = x2 - x1,
    dy = y2 - y1,
    dist = Math.sqrt(dx * dx + dy * dy);
console.log('距离为：' + dist);