NetworkX系列教程(3)-手动创建graph

小书匠Graph图论

不可否认,日常中我们使用最多的还是,使用自己的数据去手动创建自己的图形,而不是使用生成器,现从给graph添加点和边入手,讲解手动创建graph.

目录:

• 3.给graph添加节点
• 4.给graph添加边

---

注意:如果代码出现找不库,请返回第一个教程,把库文件导入.

3.给graph添加节点

1. from math import ceil 
   

   ---

2. ---

3. #该函数由于显示一组graph,传上来的是一组graph和这些graph的描述. 
   

   ---

4. def ShowGraph(glists,ginfo,rowsize=4): 
   

   ---

5. ---

6. #每行放rowsize个,计算可以放多少行 
   

   ---

7. row=ceil(len(glists)/rowsize) 
   

   ---

8. ---

9. #定义组图 
   

   ---

10. plt.subplots(row,rowsize,figsize=(15,3)) 
    

    ---

11. ---

12. #开始画图 
    

    ---

13. for ind in range(len(glists)): 
    

    ---

14. #定义子图 
    

    ---

15. plt.subplot(row,rowsize,ind+1) 
    

    ---

16. nx.draw(glists[ind],with_labels=True, font_weight='bold') 
    

    ---

17. ---

18. #设置图片 
    

    ---

19. plt.title(ginfo[ind],fontproperties=myfont) 
    

    ---

20. plt.axis('on') 
    

    ---

21. plt.xticks([]) 
    

    ---

22. plt.yticks([]) 
    

    ---

23. plt.show() 
    

    ---

1. #添加单个节点 
   

   ---

2. G1=nx.Graph() 
   

   ---

3. G1.add_node(1) 
   

   ---

4. G1.add_node("spam") 
   

   ---

5. ---

6. #添加一组节点 
   

   ---

7. G2=nx.Graph() 
   

   ---

8. G2.add_nodes_from([2, 3]) 
   

   ---

9. G2.add_nodes_from("spam") 
   

   ---

10. ---

11. #使用生成器 
    

    ---

12. G3=nx.Graph() 
    

    ---

13. H = nx.path_graph(10) 
    

    ---

14. G3.add_nodes_from(H) 
    

    ---

15. ---

16. #注意:G1.add_nodes_from(H)表示用H中的节点表示G1这个graph,如果要往G1这个graph添加H这个graph,形成graph中的graph,可以使用以下命令 
    

    ---

17. G4= nx.Graph() 
    

    ---

18. G4.add_node(1) 
    

    ---

19. G4.add_node(H) 
    

    ---

20. ---

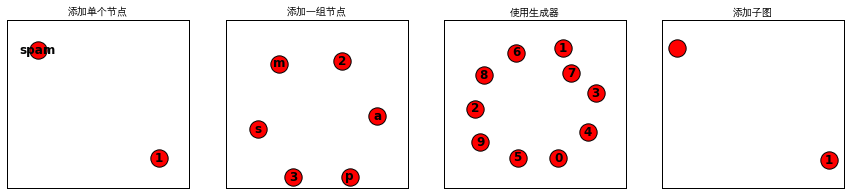
21. glists=[G1,G2,G3,G4] 
    

    ---

22. ginfo=['添加单个节点','添加一组节点','使用生成器','添加子图'] 
    

    ---

23. ShowGraph(glists,ginfo) 
    

    ---

给graph添加节点

4.给graph添加边

1. #删除前面的graph 
   

   ---

2. G1.clear() 
   

   ---

3. G2.clear() 
   

   ---

4. G3.clear() 
   

   ---

5. G4.clear() 
   

   ---

6. ---

7. #添加单边 
   

   ---

8. G1=nx.Graph() 
   

   ---

9. G1.add_edge(1,2) 
   

   ---

10. G1.add_edge(3, 'm') 
    

    ---

11. ---

12. #添加一组边 
    

    ---

13. G2=nx.Graph() 
    

    ---

14. e=(2,3) 
    

    ---

15. G2.add_edge(*e) 
    

    ---

16. ---

17. #添加多组边 
    

    ---

18. G3=nx.Graph() 
    

    ---

19. G3.add_edges_from([(3,4),(4,2)]) 
    

    ---

20. ---

21. #使用边生成器 
    

    ---

22. G4= nx.Graph() 
    

    ---

23. H = nx.path_graph(10) 
    

    ---

24. G4.add_edges_from(H.edges) 
    

    ---

25. ---

26. #添加一组有权边 
    

    ---

27. G5=nx.Graph() 
    

    ---

28. G5.add_weighted_edges_from([('a', 'b', 5.0), ('b', 'c', 3.0), ('a', 'c', 1.0), ('c', 'd', 7.3)]) #边上权重显示看设置graph信息->指定边属性 
    

    ---

29. ---

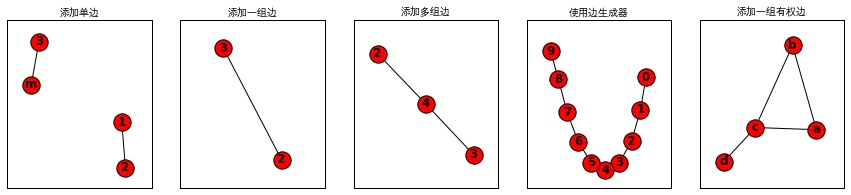
30. glists=[G1,G2,G3,G4,G5] 
    

    ---

31. ginfo=['添加单边','添加一组边','添加多组边','使用边生成器','添加一组有权边'] 
    

    ---

32. ShowGraph(glists,ginfo,rowsize=5) 
    

    ---

给graph添加边