【poj1901-求区间第k大值（带修改）】树状数组套主席树

901: Zju2112 Dynamic Rankings

Time Limit: 10 Sec  Memory Limit: 128 MB
Submit: 7025  Solved: 2925
[Submit][Status][Discuss]

Description

给定一个含有n个数的序列a[1],a[2],a[3]……a[n]，程序必须回答这样的询问：对于给定的i,j,k，在a[i],a[i+1],a[i+2]……a[j]中第k小的数是多少(1≤k≤j-i+1)，并且，你可以改变一些a[i]的值，改变后，程序还能针对改变后的a继续回答上面的问题。你需要编一个这样的程序，从输入文件中读入序列a，然后读入一系列的指令，包括询问指令和修改指令。对于每一个询问指令，你必须输出正确的回答。 第一行有两个正整数n(1≤n≤10000)，m(1≤m≤10000)。分别表示序列的长度和指令的个数。第二行有n个数，表示a[1],a[2]……a[n]，这些数都小于10^9。接下来的m行描述每条指令，每行的格式是下面两种格式中的一种。 Q i j k 或者 C i t Q i j k （i,j,k是数字，1≤i≤j≤n, 1≤k≤j-i+1）表示询问指令，询问a[i]，a[i+1]……a[j]中第k小的数。C i t (1≤i≤n，0≤t≤10^9)表示把a[i]改变成为t。

Input

对于每一次询问，你都需要输出他的答案，每一个输出占单独的一行。

Output

 

Sample Input

5 3
3 2 1 4 7
Q 1 4 3
C 2 6
Q 2 5 3

Sample Output

3
6

HINT

20%的数据中，m,n≤100; 40%的数据中，m,n≤1000; 100%的数据中，m,n≤10000。

-------------------------------------------------------------------------------------

嗷嗷嗷A了好海森

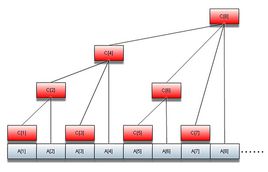
首先要回忆一下树状数组的样子。。它是一棵树的结构，也就是一个点只会被另一个点所访问到（父亲只有一个）。

上一题不带修改的主席树中，每一棵树是维护前缀区间1~L的。

这样，要是我们要修改一个数的话，就要把后面的主席树全部修改了。。复杂度变成了m*n*logn，这是不能接受的。

然后大神们就想到了树状数组！

我们修改每一棵主席树维护的区间，对于第i棵主席树，维护树状数组中所对应的lowbit(i)个数。

然后修改就只需要m*logn*logn了。

查询则变成了logn*logn的了。

 #include<cstdio>
 #include<cstdlib>
 #include<cstring>
 #include<cmath>
 #include<iostream>
 #include<algorithm>
 using namespace std;

 const int N=,INF=(int)1e9+;
 int n,m,pl,tl,mx;
 int a[*N],num[*N],crt[*N],root[*N];
 char s[];
 struct trnode{
     int lc,rc,cnt;
 }t[*N];
 struct ques{
     int l,r,k,x,d;
     bool tmp;
 }q[N];
 struct node{
     int d,id;
 }p[*N];

 bool cmp(node x,node y){return x.d<y.d;}

 int bt(int l,int r)
 {
     int x=++tl;
     t[x].cnt=;
     t[x].lc=t[x].rc=;
     if(l<r)
     {
         int mid=(l+r)/;
         t[x].lc=bt(l,mid);
         t[x].rc=bt(mid+,r);
     }
     return x;
 }

 int update(int rt,int p,int d)
 {
     int now=++tl,tmp=now;
     int l=,r=mx,mid;
     t[now].cnt=t[rt].cnt+d;
     while(l<r)
     {
         mid=(l+r)/;
         if(p<=mid)
         {
             r=mid;
             t[now].lc=++tl;
             t[now].rc=t[rt].rc;
             rt=t[rt].lc;
             now=tl;
         }
         else
         {
             l=mid+;
             t[now].lc=t[rt].lc;
             t[now].rc=++tl;
             rt=t[rt].rc;
             now=tl;
         }
         t[now].cnt=t[rt].cnt+d;
     }
     return tmp;
 }

 void add(int x,int p,int d)
 {
     for(int i=x;i<=n;i+=(i&(-i))) root[i]=update(root[i],p,d);
 }

 int getsum(int x)
 {
     int ans=;
     for(int i=x;i>=;i-=(i&(-i))) ans+=t[t[crt[i]].lc].cnt;
     return ans;
 }

 int query(int lx,int rx,int k)
 {
     for(int i=lx-;i>=;i-=(i&(-i))) crt[i]=root[i];//多棵树同时走。
     for(int i=rx;i>=;i-=(i&(-i))) crt[i]=root[i];
     int l=,r=mx,mid,sum;
     while(l<r)
     {
         mid=(l+r)/;
         sum=getsum(rx)-getsum(lx-);
         if(sum>=k)
         {
             r=mid;
             for(int i=lx-;i>=;i-=(i&(-i))) crt[i]=t[crt[i]].lc;
             for(int i=rx;i>=;i-=(i&(-i))) crt[i]=t[crt[i]].lc;
         }
         else
         {
             l=mid+;
             k-=sum;
             for(int i=lx-;i>=;i-=(i&(-i))) crt[i]=t[crt[i]].rc;
             for(int i=rx;i>=;i-=(i&(-i))) crt[i]=t[crt[i]].rc;
         }
     }
     return l;
 }

 int main()
 {
     freopen("a.in","r",stdin);
     scanf("%d%d",&n,&m);
     pl=n;tl=;
     for(int i=;i<=n;i++)
     {
         scanf("%d",&a[i]);
         p[i].d=a[i];p[i].id=i;
     }
     for(int i=;i<=m;i++)
     {
         scanf("%s",s);
         if(s[]=='Q')
         {
             q[i].tmp=;
             scanf("%d%d%d",&q[i].l,&q[i].r,&q[i].k);
         }
         else
         {
             q[i].tmp=;
             scanf("%d%d",&q[i].x,&q[i].d);
             p[++pl].d=q[i].d;p[pl].id=n+i;
         }
     }
     sort(p+,p++pl,cmp);
     mx=;p[].d=INF;
     for(int i=;i<=pl;i++)
     {
         if(p[i].d!=p[i-].d) mx++,num[mx]=p[i].d;
         if(p[i].id<=n) a[p[i].id]=mx;
         else q[p[i].id-n].d=mx;
     }
     // for(int i=1;i<=n;i++) printf("%d ",a[i]);printf("\n");
     root[]=bt(,mx);
     for(int i=;i<=n;i++)
         root[i]=root[];
     for(int i=;i<=n;i++)
         add(i,a[i],);
     for(int i=;i<=m;i++)
     {
         if(q[i].tmp==)
             printf("%d\n",num[query(q[i].l,q[i].r,q[i].k)]);
         else
         {
             add(q[i].x,a[q[i].x],-);
             add(q[i].x,q[i].d,);
             a[q[i].x]=q[i].d;//debug
         }
     }
     return ;
 }