C# 笔记——排序

首先，一张图看懂8中排序之间的关系：

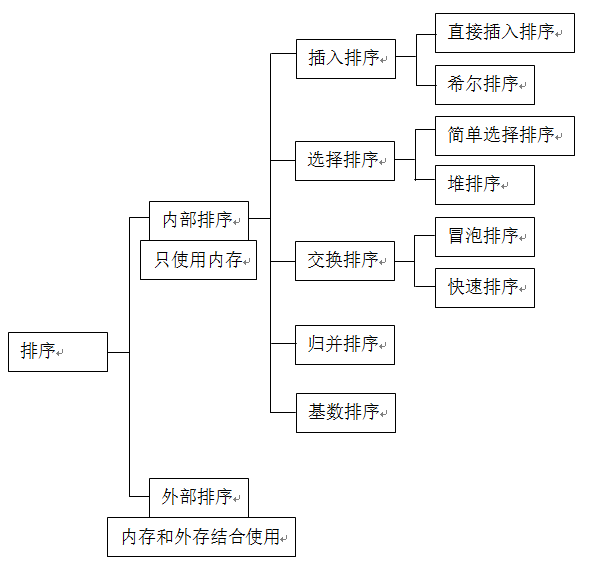
平均速度最快：快速排序

所需辅助空间最多：归并排序

所需辅助空间最少：堆排序

不稳定：快速排序，希尔排序，堆排序。

1. 直接插入排序

基本思想：在要排序的一组数中，假设前面(n-1)[n>=2] 个数已经是排好顺序的，现在要把第n个数插到前面的有序数中，使得这n个数也是排好顺序的。如此反复循环，直到全部排好顺序。

for (int i = ; i < array.Length; i++)
{
    if (array[i] > array[i - ])
    {
        int tmp = array[i];
        int j = ;
        for (j = i - ; j >=  && tmp >array[j]; --j)
        {
            array[j + ] = array[j];
        }
            array[j + ] = tmp;
    }
}

2.希尔排序（最小增量排序）

基本思想：算法先将要排序的一组数按某个增量d（n/2,n为要排序数的个数）分成若干组，每组中记录的下标相差d.对每组中全部元素进行直接插入排序，然后再用一个较小的增量（d/2）对它进行分组，在每组中再进行直接插入排序。当增量减到1时，进行直接插入排序后，排序完成。

int length = array.Length;
for (int h = length / ; h > ; h = h / )
{
    for (int i = h; i < length; i++)
    {
        T temp = array[i];
        if (temp.CompareTo(array[i -h]) < )
        {
            for (int j = ; j < i; j += h)
            {
                if (temp.CompareTo(array[j]) < )
                {
                    temp = array[j];
                    array[j] = array[i];
                    array[i] = temp;
                }
            }
        }
    }
}

3. 简单选择排序

基本思想：在要排序的一组数中，选出最小的一个数与第一个位置的数交换；然后在剩下的数当中再找最小的与第二个位置的数交换，如此循环到倒数第二个数和最后一个数比较为止。

for (int i = ; i < data.Length-; i++)
{
    int min = data[i];
    int minIndex = i;
    for (int j = i+; j < data.Length; j++)
    {
        if (data[j] <min)
        {
            min = data[j];
            minIndex = j;
        }
    }
    if (minIndex != i)
    {
        int temp = data[i];
        data[i] = data[minIndex];
        data[minIndex] = temp;
    }
}

4.  堆排序

基本思想：堆排序是一种树形选择排序，是对直接选择排序的有效改进。堆的定义如下：具有n个元素的序列（h1,h2,...,hn),当且仅当满足（hi>=h2i,hi>=2i+1）或（hi<=h2i,hi<=2i+1）(i=1,2,...,n/2)时称之为堆。在这里只讨论满足前者条件的堆。由堆的定义可以看出，堆顶元素（即第一个元素）必为最大项（大顶堆）。完全二叉树可以很直观地表示堆的结构。堆顶为根，其它为左子树、右子树。初始时把要排序的数的序列看作是一棵顺序存储的二叉树，调整它们的存储序，使之成为一个堆，这时堆的根节点的数最大。然后将根节点与堆的最后一个节点交换。然后对前面(n-1)个数重新调整使之成为堆。依此类推，直到只有两个节点的堆，并对它们作交换，最后得到有n个节点的有序序列。从算法描述来看，堆排序需要两个过程，一是建立堆，二是堆顶与堆的最后一个元素交换位置。所以堆排序有两个函数组成。一是建堆的渗透函数，二是反复调用渗透函数实现排序的函数。

static void HeapAdjust(List<int> list,int parent,int length)
{
    int temp=list[parent];//parent是索引
    int child =  * parent + ;
    while (child < length)
    {
        if (child +  < length && list[child] < list[child + ]) child++;
        if (temp >= list[child])
            break;
        list[parent] = list[child];
        parent = child;
        child =  * parent + ;
    }
    list[parent] = temp;
}
public static List<int> HeapSort(List<int> list, int top)
{
    List<int> topNode = new List<int>();
    for (int i = list.Count /  - ; i >= ; i--)
    {
        HeapAdjust(list, i, list.Count);//最大堆
    }
    for (int i = list.Count - ; i >= list.Count - top; i--)
    {
        int temp = list[];
        list[] = list[i];
        list[i] = temp;
        topNode.Add(temp);
        HeapAdjust(list, , i);
    }
    return topNode;
}

5.冒泡排序

基本思想：在要排序的一组数中，对当前还未排好序的范围内的全部数，自上而下对相邻的两个数依次进行比较和调整，让较大的数往下沉，较小的往上冒。即：每当两相邻的数比较后发现它们的排序与排序要求相反时，就将它们互换。

int[] numbers = { , , , , , , , , ,  };  //定义一个要排序的数组，这里可以随便写多少个数
for (int i = ; i < numbers.Length - ; i++)  //外层 循环比较遍数
{
    for (int j = ; j < numbers.Length -  - i; j++)
    {
        if (numbers[j] > numbers[j + ])  //两个数进行比较，如果大于就交换
        {
            int temp = numbers[j]; //temp 两个数交换时要有第三个数来过度
            numbers[j] = numbers[j + ];
            numbers[j + ] = temp;
        }
    }
}

6.快速排序

基本思想：选择一个基准元素,通常选择第一个元素或者最后一个元素,通过一趟扫描，将待排序列分成两部分,一部分比基准元素小,一部分大于等于基准元素,此时基准元素在其排好序后的正确位置,然后再用同样的方法递归地排序划分的两部分。

private static int QuickSort_Once(int[] _pnArray, int _pnLow, int _pnHigh)
{
    int nPivot = _pnArray[_pnLow];
    int i = _pnLow, j = _pnHigh;
    while (i < j)
    {
        while (_pnArray[j] >= nPivot && i<j) j--;
        _pnArray[i] = _pnArray[j];
        while (_pnArray[i] <= nPivot && i<j) i++;
        _pnArray[j] = _pnArray[i];
    }
    _pnArray[i] = nPivot;
    return i;
}
private static void QuickSort(int[] _pnArray, int _pnLow, int _pnHigh)
{
    if (_pnLow >= _pnHigh) return;
    int _nPivotIndex = QuickSort_Once(_pnArray, _pnLow, _pnHigh);
    QuickSort(_pnArray, _pnLow, _nPivotIndex-);
    QuickSort(_pnArray, _nPivotIndex + ,_pnHigh);
}

7.归并排序

基本思想：归并（Merge）排序法是将两个（或两个以上）有序表合并成一个新的有序表，即把待排序序列分为若干个子序列，每个子序列是有序的。然后再把有序子序列合并为整体有序序列。

//归并排序（目标数组，子表的起始位置，子表的终止位置）
private static void MergeSortFunction(int[] array, int first, int last)
{
    try
    {
        if (first < last)   //子表的长度大于1，则进入下面的递归处理
        {
            int mid = (first + last) / ;   //子表划分的位置
            MergeSortFunction(array, first, mid);   //对划分出来的左侧子表进行递归划分
            MergeSortFunction(array, mid + , last);    //对划分出来的右侧子表进行递归划分
            MergeSortCore(array, first, mid, last); //对左右子表进行有序的整合（归并排序的核心部分）
        }
    }
    catch (Exception ex)
    { }
}
//归并排序的核心部分：将两个有序的左右子表（以mid区分），合并成一个有序的表
private static void MergeSortCore(int[] array, int first, int mid, int last)
{
    try
    {
        int indexA = first; //左侧子表的起始位置
        int indexB = mid + ;   //右侧子表的起始位置
        int[] temp = new int[last + ]; //声明数组（暂存左右子表的所有有序数列）：长度等于左右子表的长度之和。
        int tempIndex = ;
        while (indexA <= mid && indexB <= last) //进行左右子表的遍历，如果其中有一个子表遍历完，则跳出循环
        {
            if (array[indexA] <= array[indexB]) //此时左子表的数 <= 右子表的数
            {
                temp[tempIndex++] = array[indexA++];    //将左子表的数放入暂存数组中，遍历左子表下标++
            }
            else//此时左子表的数 > 右子表的数
            {
                temp[tempIndex++] = array[indexB++];    //将右子表的数放入暂存数组中，遍历右子表下标++
            }
        }
        //有一侧子表遍历完后，跳出循环，将另外一侧子表剩下的数一次放入暂存数组中（有序）
        while (indexA <= mid)
        {
            temp[tempIndex++] = array[indexA++];
        }
        while (indexB <= last)
        {
            temp[tempIndex++] = array[indexB++];
        }
        //将暂存数组中有序的数列写入目标数组的制定位置，使进行归并的数组段有序
        tempIndex = ;
        for (int i = first; i <= last; i++)
        {
            array[i] = temp[tempIndex++];
        }
    }
    catch (Exception ex)
    { }
}

8.基数排序

基本思想：将所有待比较数值（正整数）统一为同样的数位长度，数位较短的数前面补零。然后，从最低位开始，依次进行一次排序。这样从最低位排序一直到最高位排序完成以后,数列就变成一个有序序列。

public static int[] RadixSort(int[] ArrayToSort, int digit)
{
    //low to high digit
    for (int k = ; k <= digit; k++)
    {
        //temp array to store the sort result inside digit
        int[] tmpArray = new int[ArrayToSort.Length];

        //temp array for countingsort
        int[] tmpCountingSortArray = new int[]{,,,,,,,,,};

        //CountingSort
        for (int i = ; i < ArrayToSort.Length; i++)
        {
            //split the specified digit from the element
            int tmpSplitDigit = ArrayToSort[i]/(int)Math.Pow(,k-) - (ArrayToSort[i]/(int)Math.Pow(,k))*;
            tmpCountingSortArray[tmpSplitDigit] += ;
        }

        for (int m = ; m < ; m++)
        {
            tmpCountingSortArray[m] += tmpCountingSortArray[m - ];
        }

        //output the value to result
        for (int n = ArrayToSort.Length - ; n >= ; n--)
        {
            int tmpSplitDigit = ArrayToSort[n] / (int)Math.Pow(,k - ) - (ArrayToSort[n]/(int)Math.Pow(,k)) * ;
            tmpArray[tmpCountingSortArray[tmpSplitDigit]-] = ArrayToSort[n];
            tmpCountingSortArray[tmpSplitDigit] -= ;
        }

        //copy the digit-inside sort result to source array
        for (int p = ; p < ArrayToSort.Length; p++)
        {
            ArrayToSort[p] = tmpArray[p];
        }
    }

    return ArrayToSort;
}