leetcode28 strstr kmp bm sunday

字符串匹配有KMP，BM,SUNDAY算法。

可见（https://leetcode-cn.com/problems/implement-strstr/solution/c5chong-jie-fa-ku-han-shu-bfkmpbmsunday-by-2227/）

https://www.cnblogs.com/ZuoAndFutureGirl/p/9028287.html

KMP核心就是next数组(pattern接下来向后移动的位数) (text 当前匹配到的index不变)

模式串向右移动的位数为：失配字符所在位置 - 失配字符对应的next 值

即移动的实际位数为：j - next[j]，且此值大于等于1。

操作为

if(text[i]!=p[j])

j=next[j];  //  next[j] 即为p[0,j-1]串中最长前后缀长度.   p[j]与text[i]失配,但text[X,i-1]与p[0,j-1]匹配,其中最长前后缀也匹配,直接移动pattern,前缀覆盖后缀,比较下一位p[k]与text[i]是否匹配

//p[next[j]] 即为最长前后缀后面一位p[k]

//k为 next[j]. 即p[0,j-1]串最长前后缀的长度

next求法:

next[0]=-1  //若text[i]与pattern第一个字符失配,直接向后移动pattern一位

k =next [j]  // j-1串中,最长的前后缀长度为k

if p[j]==p[k] //j串中最长前后缀长度为k+1

next[j + 1] = next[j] + 1

else

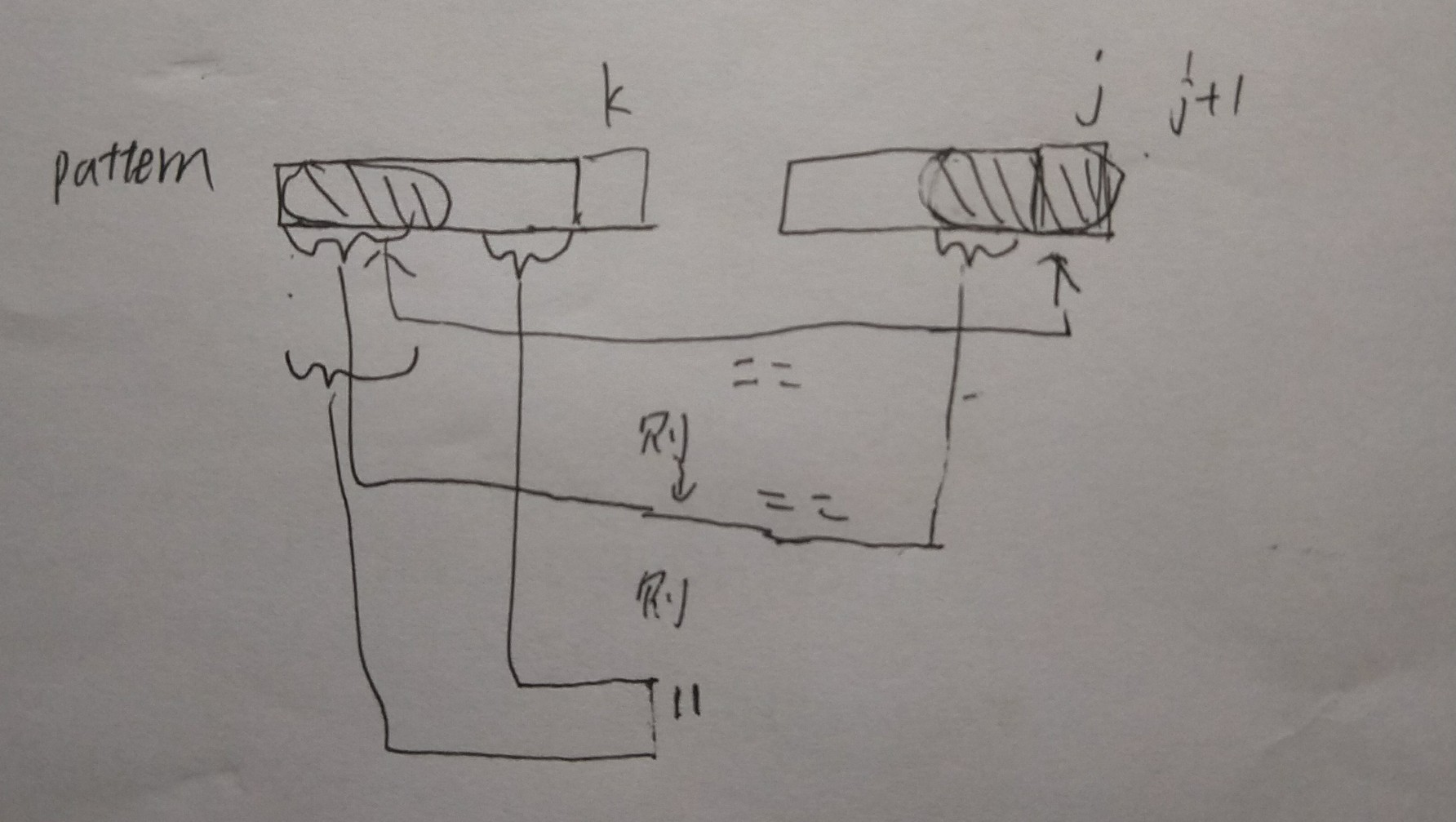
k=next[k]  //画个图就很好想.

void GetNext(char* p,int next[])
{
    int pLen = strlen(p);
    next[0] = -1;
    int k = -1;
    int j = 0;
    while (j < pLen - 1)
    {
        //p[k]表示前缀，p[j]表示后缀
        if (k == -1 || p[j] == p[k])
        {
            ++k;
            ++j;
            next[j] = k;
        }
        else
        {
            k = next[k];
        }
    }
}  

next优化:

问题出在不该出现p[j] = p[ next[j] ]。

理由是：当p[j] != text[i] 时，下次匹配必然是p[ next [j]] 跟text[i]匹配，如果p[j] = p[ next[j] ]，必然导致后一步匹配失败

（因为p[j]已经跟s[i]失配，然后你还用跟p[j]等同的值p[next[j]]去跟s[i]匹配，很显然，必然失配），

所以不能允许p[j] = p[ next[j ]]。如果出现了p[j] = p[ next[j] ],则需要再次递归，即令next[j] = next[ next[j] ]。

所以，咱们得修改下求next 数组的代码。

//优化过后的next 数组求法
void GetNextval(char* p, int next[])
{
    int pLen = strlen(p);
    next[0] = -1;
    int k = -1;
    int j = 0;
    while (j < pLen - 1)
    {
        //p[k]表示前缀，p[j]表示后缀
        if (k == -1 || p[j] == p[k])
        {
            ++j;
            ++k;
            //较之前next数组求法，改动在下面4行
            if (p[j] != p[k])
                next[j] = k;   //之前只有这一行
            else
                //因为不能出现p[j] = p[ next[j ]]，所以当出现时需要继续递归，k = next[k] = next[next[k]]
                next[j] = next[k];
        }
        else
        {
            k = next[k];
        }
    }
}  

因为比较熟悉KMP，就用KMP了

class Solution {
public:
    vector<int> getnext(string str)
        {
            int len=str.size();
            vector<int> next;
            next.push_back(-1);//next数组初值为-1
            int j=0,k=-1;
            while(j<len-1)
            {
                if(k==-1||str[j]==str[k])//str[j]后缀 str[k]前缀
                {
                    j++;
                    k++;
                    if(str[j]!=str[k])
                        next.push_back(k);
                    else
                        next.push_back(next[k]);
                }
                else
                {
                    k=next[k];
                }
            }
            return next;
        }

    int strStr(string haystack, string needle) {
        if(needle.empty())
            return 0;

        int i=0;
        int j=0;
        int len1=haystack.size();
        int len2=needle.size();
        vector<int> next;
        next=getnext(needle);
        while((i<len1)&&(j<len2))
        {
            if((j==-1)||(haystack[i]==needle[j]))
            {
                i++;
                j++;
            }
            else
            {
                j=next[j];//获取下一次匹配的位置
            }
        }
        if(j==len2)
            return i-j;

        return -1;
    }

};

然后看题解，有SunDay算法，更好理解（https://leetcode-cn.com/problems/implement-strstr/solution/python3-sundayjie-fa-9996-by-tes/）

偏移表告诉我们下一步可能匹配需要移动的最小步数

设text，patternlen=len

核心思想就是当前匹配若失败，那么当前text中开始匹配的位置i+len-1必不可能匹配上。此时检查i+len处的字符，当其等于pattern中的某个字符（从右向左找），则将pattern移动使text[i+len]与pattern中相应字符对应。

然后重复。

若没有匹配上，那么直接移动len+1

最坏情况：O(nm)
平均情况：O(n)

（实际提交的 时候，确实sunday比kmp快一点。可能是测试用例的关系）

class Solution {
public:
    int strStr(string haystack, string needle) {
        if(needle.empty())
            return 0;
        int slen=haystack.size();
        int tlen=needle.size();
        if(slen<tlen)
            return -1;
        int i=0,j=0;//i指向源串首位 j指向子串首位
        int k;
        int m=tlen;//第一次匹配时 源串中参与匹配的元素的下一位

        while(i<slen)
        {
            if(haystack[i]!=needle[j])
            {
                for(k=tlen-1;k>=0;k--)//遍历查找此时pattern与源串[i+tlen+1]相等的最右位置
                {
                    if(needle[k]==haystack[m])
                        break;
                }
                i=m-k;//i为下一次匹配源串开始首位 Sunday算法核心：最大限度跳过相同元素
                j=0;//j依然为子串首位
                m=i+tlen;//m为下一次参与匹配的源串最后一位元素的下一位
                if(m>slen)
                    return -1;
            }
            else
            {
                if(j==tlen-1)//若j为子串末位 匹配成功 返回源串此时匹配首位
                    return i-j;
                i++;
                j++;
            }
        }
        return -1;//当超过源串长度时
    }
};

还有bm算法 O(N) - O(M+N)

class Solution {
public:
    void get_bmB(string& T,vector<int>& bmB)//坏字符
    {
        int tlen=T.size();
        for(int i=0;i<256;i++)//不匹配直接移动子串
        {
            bmB.push_back(tlen);
        }
        for(int i=0;i<tlen-1;i++)//靠右原则
        {
            bmB[T[i]]=tlen-i-1;
        }
    }

    void get_suff(string& T,vector<int>& suff)
    {
        int tlen=T.size();
        int k;
        for(int i=tlen-2;i>=0;i--)
        {
            k=i;
            while(k>=0&&T[k]==T[tlen-1-i+k])
                k--;
            suff[i]=i-k;
        }
    }

    void get_bmG(string& T,vector<int>& bmG)//好后缀
    {
        int i,j;
        int tlen=T.size();
        vector<int> suff(tlen+1,0);
        get_suff(T,suff);//suff存储子串的最长匹配长度
        //初始化 当没有好后缀也没有公共前缀时
        for(i=0;i<tlen;i++)
            bmG[i]=tlen;
        //没有好后缀 有公共前缀 调用suff 但是要右移一位 类似KMP里的next数组
        for(i=tlen-1;i>=0;i--)
            if(suff[i]==i+1)
                for(j=0;j<tlen-1;j++)
                    if(bmG[j]==tlen)//保证每个位置不会重复修改
                        bmG[j]=tlen-1-i;
        //有好后缀 有公共前缀
        for(i=0;i<tlen-1;i++)
            bmG[tlen-1-suff[i]]=tlen-1-i;//移动距离
    }

    int strStr(string haystack, string needle) {

        int i=0;
        int j=0;
        int tlen=needle.size();
        int slen=haystack.size();

        vector<int> bmG(tlen,0);
        vector<int> bmB;
        get_bmB(needle,bmB);
        get_bmG(needle,bmG);

        while(i<=slen-tlen)
        {
            for(j=tlen-1;j>-1&&haystack[i+j]==needle[j];j--);
            if(j==(-1))
                return i;
            i+=max(bmG[j],bmB[haystack[i+j]]-(tlen-1-j));
        }
        return -1;
    }
};

作者：2227
链接：https://leetcode-cn.com/problems/implement-strstr/solution/c5chong-jie-fa-ku-han-shu-bfkmpbmsunday-by-2227/
来源：力扣（LeetCode）
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。