CodeForces - 1100E 二分+拓扑排序

题意：

一个n个节点的有向图，节点标号从1到n，存在m条单向边。每条单向边有一个权值，代表翻转其方向所需的代价。求使图变成无环图，其中翻转的最大边权值最小的方案，以及该方案翻转的最大的边权。

Input

单组输入，第一行包含两个整数n和m(2≤n≤100 000,1≤m≤100 000) 接下来m行，每行3个整数，u_i ，v_i，w_i （1<= u_i , v_i <= n, 1<= w_i <=10^9），表示u到v有一条权值为w的道路。道路编号从1开始。没有自环。

Output

在第一行中输出两个整数，即要翻转的最大的边权，和需要反转道路数量k。k不需要是最小的。

在下一行输出k个由空格分隔的整数，表示需要翻转的道路编号

如果有许多解决方案，请打印其中任何一个。

题解：

这是一个通过拓扑来使一个图变成无环图的相关链接：https://www.geeksforgeeks.org/assign-directions-to-edges-so-that-the-directed-graph-remains-acyclic/

这个链接的结论就是如果一个有向图图是一个无环图，那么对于每一条有向边<x,y>，点x在拓扑排序的结构中的位置肯定要比y靠前，就像下面这个图

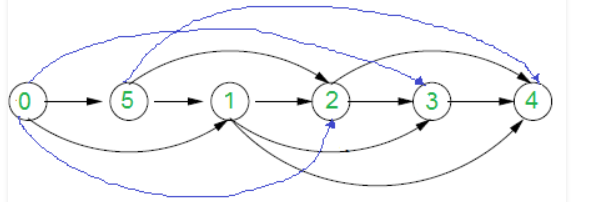
回归本题，我们可以二分枚举那个最大的权值，那么小于这个权值的边都可以看做为无向边（就当作这些边都不存在），对剩下的边进行一次拓扑排序。然后这n个点就会有一个顺序，之后就根据上面的那个结论来判断这些无向边的指向应该怎么指才不会构成有环图，如果边的指向和题上输入的相反就记录一下输出

代码：

 1 #include <cstdio>
 2 #include <cstring>
 3 #include <cctype>
 4 #include<queue>
 5 #include<vector>
 6 #include<iostream>
 7 #include <algorithm>
 8 using namespace std;
 9 const int maxn=1e5+10;
10 typedef long long LL;
11 const int MAX=1e5+10;
12 const int MOD=1e9+7;
13 const int INF=1e9+7;
14 typedef long long ll;
15 struct lenka{int x,y,z;}ed[MAX];
16 vector<int>e[MAX];
17 vector<int>QAQ;
18 int top[MAX],in[MAX];
19 int n,m;
20 int check(int QWQ)
21 {
22     for(int i=1;i<=n;i++)e[i].clear();
23     memset(in,0,sizeof in);
24     for(int i=1;i<=m;i++)
25     {
26         if(ed[i].z>QWQ)
27         {
28             e[ed[i].x].push_back(ed[i].y);
29             ++in[ed[i].y];
30         }
31     }
32     queue<int>p;
33     int cnt=0;
34     for(int i=1;i<=n;i++)if(in[i]==0)p.push(i),top[i]=++cnt;
35     while(!p.empty())
36     {
37         int now=p.front();p.pop();
38         for(int i=0;i<e[now].size();i++)
39         {
40             int nex=e[now][i];
41             in[nex]--;
42             if(in[nex]==0)
43             {
44                 p.push(nex);
45                 top[nex]=++cnt;
46             }
47         }
48     }
49     for(int i=1;i<=n;i++)if(in[i])return 0;
50     QAQ.clear();
51     for(int i=1;i<=m;i++)if(ed[i].z<=QWQ&&top[ed[i].y]<top[ed[i].x])QAQ.push_back(i);
52     return 1;
53 }
54 int main()
55 {
56     cin>>n>>m;
57     for(int i=1;i<=m;i++)scanf("%d%d%d",&ed[i].x,&ed[i].y,&ed[i].z);
58     int l=0,r=1e9,ans=0;
59     while(r>=l)
60     {
61         int mid=(l+r)/2;
62         if(check(mid))r=mid-1,ans=mid;
63         else l=mid+1;
64     }
65     check(ans);
66     printf("%d %d\n",ans,QAQ.size());
67     for(int i=0;i<QAQ.size();i++)cout<<QAQ[i]<<" ";
68     return 0;
69 }