《神经网络的梯度推导与代码验证》之vanilla RNN的前向传播和反向梯度推导

在本篇章，我们将专门针对vanilla RNN，也就是所谓的原始RNN这种网络结构进行前向传播介绍和反向梯度推导。更多相关内容请见《神经网络的梯度推导与代码验证》系列介绍。

注意：

• 本系列的关注点主要在反向梯度推导以及代码上的验证，涉及到的前向传播相对而言不会做太详细的介绍。
• 反向梯度求导涉及到矩阵微分和求导的相关知识，请见《神经网络的梯度推导与代码验证》之数学基础篇：矩阵微分与求导

---

目录

• 4.1 vanilla RNN的前向传播
• 4.2 vanilla RNN的反向梯度推导
• 4.3 vanilla RNN发送梯度消失与梯度爆炸的原因分析
• 参考资料

提醒：

• 后续会反复出现$\boldsymbol{\delta}^{l}$这个（类）符号，它的定义为$\boldsymbol{\delta}^{l} = \frac{\partial l}{\partial\boldsymbol{z}^{\boldsymbol{l}}}$，即loss $l$对$\boldsymbol{z}^{\boldsymbol{l}}$的导数
• 其中$\boldsymbol{z}^{\boldsymbol{l}}$表示第$l$层（DNN，CNN，RNN或其他例如max pooling层等）未经过激活函数的输出。
• $\boldsymbol{a}^{\boldsymbol{l}}$则表示$\boldsymbol{z}^{\boldsymbol{l}}$经过激活函数后的输出。

这些符号会贯穿整个系列，还请留意。

---

 

4.1 vanilla RNN的前向传播

先贴一张vanilla（朴素）RNN的前传示意图。

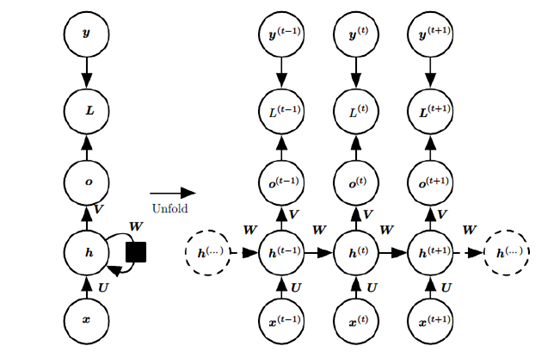
上图中左边是RNN模型没有按时间展开的图，如果按时间序列展开，则是上图中的右边部分。我们重点观察右边部分的图。这幅图描述了在序列索引号t附近RNN的模型。其中：

• $\boldsymbol{x}^{(t)}$代表在序列索引号$t$时训练样本的输入。注意这里的$t$只是代表序列索引，不一定非得具备时间上的含义，例如$\boldsymbol{x}^{(t)}$可以是某句子的第$t$个字（的词向量）。
• $\boldsymbol{h}^{(t)}$代表在序列索引号$t$时模型的隐藏状态。$\boldsymbol{h}^{(t)}$由$\boldsymbol{x}^{(t)}$和$\boldsymbol{h}^{(t-1)}$共同决定
• $\boldsymbol{a}^{(t)}$代表在序列索引号$t$时模型的输出。$\boldsymbol{o}^{(t)}$只由模型当前的隐藏状态$\boldsymbol{h}^{(t-1)}$决定
• $\boldsymbol{L}^{(t)}$代表在序列索引号$t$时模型的损失函数。
• $\boldsymbol{y}^{(t)}$代表在序列索引号$t$时训练样本序列的真实输出
• $\boldsymbol{U},\boldsymbol{W},\boldsymbol{V}$三个矩阵式我们模型的线性相关系数，它们在整个vanilla RNN网络中共享的，这点和DNN很不同。也正因为是共享的，它体现了RNN模型的“循环/递归”的核心思想。

4.1.1 RNN前向传播计算公式

有了上面的模型，RNN的前向传播算法就很容易得到了。

对于任意一个序列索引号$t$，我们隐藏状态$\boldsymbol{h}^{(t)}$由$\boldsymbol{x}^{(t)}$和$\boldsymbol{h}^{(t-1)}$共同得到：

$\boldsymbol{h}^{(t)} = \sigma\left( \boldsymbol{z}^{(t)} \right) = \sigma\left( {\boldsymbol{U}\boldsymbol{x}^{(t)} + \boldsymbol{W}\boldsymbol{h}^{(t - 1)} + \boldsymbol{b}} \right)$

其中$\sigma$为RNN的激活函数，一般为$tanh$。

序列索引号为$t$时，模型的输出$\boldsymbol{o}^{(t)}$的表达式也比较简单：

$\boldsymbol{o}^{(t)} = \boldsymbol{V}\boldsymbol{h}^{(t - 1)} + \boldsymbol{c}$

在最终在序列索引号t

时我们的预测输出为：

${\hat{\boldsymbol{y}}}^{(t)} = \sigma\left( \boldsymbol{o}^{(t)} \right)$

对比下列公式：

$\boldsymbol{h}^{(t)} = \sigma\left( {\boldsymbol{U}\boldsymbol{x}^{(t)} + \boldsymbol{W}\boldsymbol{h}^{(t - 1)} + \boldsymbol{b}} \right)$

$\boldsymbol{a}^{l} = \sigma\left( {\boldsymbol{W}^{l}\boldsymbol{a}^{l - 1} + \boldsymbol{b}^{l}} \right)$

上面的是vanilla RNN的$\boldsymbol{h}^{(t)}$的递推公式，而下面的是DNN中的层间关系的公式。我们可以发现这两组公式在形式上非常接近。如果将$\boldsymbol{h}^{(t)}$的这种时间上的展开看成类似于DNN这种层间堆叠的话，可以发现vanilla RNN每一“层”除了有来自上一“层”的输入$\boldsymbol{h}^{(t - 1)}$，还有专属于这一层的输入$\boldsymbol{x}^{(t)}$，最重要的是，每一“层”的参数$\boldsymbol{W}$和$\boldsymbol{b}$都是同一组。而DNN则是有专属于那一层的$\boldsymbol{W}^{l}$和$\boldsymbol{b}^{l}$。

---

4.2 vanilla RNN的反向梯度推导

RNN反向传播算法的思路和DNN是一样的，即通过梯度下降法一轮轮的迭代，得到合适的RNN模型参数$\boldsymbol{U},\boldsymbol{W},\boldsymbol{V},\boldsymbol{b},\boldsymbol{c}$。由于我们是基于时间反向传播，所以RNN的反向传播有时也叫做BPTT(back-propagation through
time)。当然这里的BPTT和DNN也有很大的不同点，即这里所有的$\boldsymbol{U},\boldsymbol{W},\boldsymbol{V},\boldsymbol{b},\boldsymbol{c}$在序列的各个位置是共享的，反向传播时我们更新的是相同的参数。

为了简化描述，这里的损失函数我们为交叉熵损失函数，输出的激活函数为softmax函数，隐藏层的激活函数为tanh函数。

如果RNN在序列t

的每个位置有输出，则最终的损失L为所有时间步$t$的loss之和：

$L = {\sum\limits_{t = 1}^{T}L^{(t)}}$

其中，$\boldsymbol{V},\boldsymbol{c}$的梯度计算比较简单，跟求DNN的BP是一样的。

根据 数学基础篇：矩阵微分与求导 1.8节例子的中间结果，我们可以知道：

$\frac{\partial L}{\partial\boldsymbol{c}} = {\sum\limits_{t = 1}^{T}\frac{\partial L^{(t)}}{\partial\boldsymbol{c}}} = {\sum\limits_{t = 1}^{T}{{\hat{\boldsymbol{y}}}^{(t)} - \boldsymbol{y}^{(t)}}}$

$\frac{\partial L}{\partial\boldsymbol{V}} = {\sum\limits_{t = 1}^{T}\frac{\partial L^{(t)}}{\partial\boldsymbol{V}}} = {\sum\limits_{t = 1}^{T}\left( {{\hat{\boldsymbol{y}}}^{(t)} - \boldsymbol{y}^{(t)}} \right)}\left( \boldsymbol{h}^{(t)} \right)^{T}$

接下来的$\boldsymbol{U},\boldsymbol{W},\boldsymbol{b}$的梯度计算就相对复杂了。从RNN的模型可以看出，在反向传播时，某一序列位置$t$的梯度由当前位置的输出对应的梯度和序列索引位置$t+1$时的梯度两部分共同决定。对于$\boldsymbol{W}$在某一序列位置$t$的梯度损失需要反向传播一步一步地计算。我们定义序列索引$t$位置的隐藏状态的梯度为：

$\boldsymbol{\delta}^{(t)} = \frac{\partial L}{\partial\boldsymbol{h}^{(t)}}$

如果我们能知道$\boldsymbol{\delta}^{(t)}$，那么根据$\boldsymbol{h}^{(t)} = \sigma\left( \boldsymbol{z}^{(t)} \right) = \sigma\left( {\boldsymbol{U}\boldsymbol{x}^{(t)} + \boldsymbol{W}\boldsymbol{h}^{(t - 1)} + \boldsymbol{b}} \right)$我们就像DNN那样套用标量对矩阵的链式求导法则来进一步得到$\boldsymbol{U},\boldsymbol{W},\boldsymbol{b}$的梯度了。

根据4.1节中的示意图我们可以轻易发现，当$t = T$，则误差只有$\left. L^{(T)}\rightarrow\boldsymbol{h}^{(T)} \right.$这么一条。

所以：

$\boldsymbol{\delta}^{(T)} = \boldsymbol{V}^{T}\left( {{\hat{\boldsymbol{y}}}^{(T)} - \boldsymbol{y}^{(T)}} \right)$

而当$t<T$时，$\boldsymbol{h}^{(t)}$的误差来源有两条：

1)$\left. L^{(t)}\rightarrow\boldsymbol{h}^{(t)} \right.$

2)$\left. \boldsymbol{h}^{({t + 1})}\rightarrow\boldsymbol{h}^{(t)} \right.$

于是我们得到：

$\boldsymbol{\delta}^{(t)} = \frac{\partial L^{(t)}}{\partial\boldsymbol{h}^{(t)}} + \left( \frac{\partial\boldsymbol{h}^{(t + 1)}}{\partial\boldsymbol{h}^{(t)}} \right)^{T}\frac{\partial L}{\partial\boldsymbol{h}^{(t + 1)}}$

我们来逐项求解：

首先对于$\frac{\partial L^{(t)}}{\partial\boldsymbol{h}^{(t)}}$:

$\boldsymbol{\delta}^{(t)} = \frac{\partial L}{\partial\boldsymbol{h}^{(t)}} = \left( \frac{\partial\boldsymbol{o}^{(t)}}{\partial\boldsymbol{h}^{(t)}} \right)^{T}\frac{\partial L}{\partial\boldsymbol{o}^{(t)}} = \boldsymbol{V}^{T}\left( {{\hat{\boldsymbol{y}}}^{(t)} - \boldsymbol{y}^{(t)}} \right)$

对于$\left( \frac{\partial\boldsymbol{h}^{(t + 1)}}{\partial\boldsymbol{h}^{(t)}} \right)^{T}\frac{\partial L^{({t + 1})}}{\partial\boldsymbol{h}^{(t + 1)}}$，我们先关注$\frac{\partial\boldsymbol{h}^{(t + 1)}}{\partial\boldsymbol{h}^{(t)}}$：

因为$\boldsymbol{h}^{(t + 1)} = \sigma\left( \boldsymbol{z}^{(t)} \right) = \sigma\left( {\boldsymbol{U}\boldsymbol{x}^{(t + 1)} + \boldsymbol{W}\boldsymbol{h}^{(t)} + \boldsymbol{b}} \right)$

所以有：

$d\boldsymbol{h}^{(t + 1)} = \sigma^{'}\left( \boldsymbol{h}^{(t + 1)} \right)\bigodot d\boldsymbol{z}^{(t)} = diag\left( {\sigma^{'}\left( \boldsymbol{h}^{({t + 1})} \right)} \right)d\boldsymbol{z}^{(t)} = diag\left( {\sigma^{'}\left( \boldsymbol{h}^{({t + 1})} \right)} \right)d\left( {\boldsymbol{W}\boldsymbol{h}^{(t)}} \right) = diag\left( {\sigma^{'}\left( \boldsymbol{h}^{({t + 1})} \right)} \right)\boldsymbol{W}d\boldsymbol{h}^{(t)}$

所以有：$\frac{\partial\boldsymbol{h}^{(t + 1)}}{\partial\boldsymbol{h}^{(t)}} = diag\left( {\sigma^{'}\left( \boldsymbol{h}^{({t + 1})} \right)} \right)\boldsymbol{W}$

于是：

$\boldsymbol{\delta}^{(t)} = \boldsymbol{V}^{T}\left( {{\hat{\boldsymbol{y}}}^{(t)} - \boldsymbol{y}^{(t)}} \right) + \boldsymbol{W}^{T}diag\left( {\sigma^{'}\left( \boldsymbol{h}^{(t + 1)} \right)} \right)\boldsymbol{\delta}^{(t + 1)}$

有了$\boldsymbol{\delta}^{(T)}$以及从$\boldsymbol{\delta}^{(t + 1)}$到$\boldsymbol{\delta}^{(t)}$的递推公式，我们可以轻易求出$\boldsymbol{U},\boldsymbol{W},\boldsymbol{b}$的梯度，由于这三组变量在不同的$t$下是公用的，所以由全微分方程可知，这三个变量应当都是在$t$上的某种累加形式。我们定义只在时间步$t$使用的虚拟变量$\boldsymbol{U}^{(t)},\boldsymbol{W}^{(t)},\boldsymbol{b}^{(t)}$，这样就可以用$\frac{\partial L}{\partial\boldsymbol{W}^{(t)}}$来表示$\boldsymbol{W}$在时间步$t$的时候对梯度的贡献：

$\frac{\partial L}{\partial\boldsymbol{W}} = {\sum\limits_{t = 1}^{T}\frac{\partial L}{\partial\boldsymbol{W}^{(t)}}} = {\sum\limits_{t = 1}^{T}{\left( \frac{\partial\boldsymbol{h}^{(t)}}{\partial\boldsymbol{W}^{(t)}} \right)^{T}\frac{\partial L}{\partial\boldsymbol{h}^{(t)}} =}}{\sum\limits_{t = 1}^{T}{diag\left( {\sigma^{'}\left( \boldsymbol{h}^{(t + 1)} \right)} \right)\boldsymbol{\delta}^{(t)}\left( \boldsymbol{h}^{(t - 1)} \right)^{T}}}$

同理，我们得到：

$\frac{\partial L}{\partial\boldsymbol{b}} = {\sum\limits_{t = 1}^{T}{\frac{\partial L}{\partial\boldsymbol{b}^{(t)}} =}}{\sum\limits_{t = 1}^{T}{\left( \frac{\partial\boldsymbol{h}^{(t)}}{\partial\boldsymbol{b}^{(t)}} \right)^{T}\frac{\partial L}{\partial\boldsymbol{h}^{(t)}} = {\sum\limits_{t = 1}^{T}{diag\left( {\sigma^{'}\left( \boldsymbol{h}^{(t + 1)} \right)} \right)\boldsymbol{\delta}^{(t)}}}}}$

$\frac{\partial L}{\partial\boldsymbol{U}} = {\sum\limits_{t = 1}^{T}{\frac{\partial L}{\partial\boldsymbol{U}^{(t)}} =}}{\sum\limits_{t = 1}^{T}{\left( \frac{\partial\boldsymbol{h}^{(t)}}{\partial\boldsymbol{U}^{(t)}} \right)^{T}\frac{\partial L}{\partial\boldsymbol{h}^{(t)}} = {\sum\limits_{t = 1}^{T}{diag\left( {\sigma^{'}\left( \boldsymbol{h}^{(t + 1)} \right)} \right)\boldsymbol{\delta}^{(t)}\left( \boldsymbol{x}^{(t)} \right)^{T}}}}}$

---

4.3 RNN发生梯度消失与梯度爆炸的原因分析

上一节我们得到了从$\boldsymbol{h}^{(t + 1)}$到$\boldsymbol{h}^{(t)}$的递推公式：

$\frac{\partial\boldsymbol{h}^{(t + 1)}}{\partial\boldsymbol{h}^{(t)}} = diag\left( {\sigma^{'}\left( \boldsymbol{h}^{({t + 1})} \right)} \right)\boldsymbol{W}$

在求$\boldsymbol{h}^{(t)}$的时候，我们需要从$\boldsymbol{h}^{(T)}$开始根据上面这个公式一步一步推到$\boldsymbol{h}^{(t)}$，可以想象$\boldsymbol{W}$在这期间会被疯狂地连乘。当我们要求某个时间步$t$下的$\frac{\partial L}{\partial\boldsymbol{W}^{(t)}}$时，这一堆连乘的$\boldsymbol{W}$也会被带上。结果就是（粗略地分析），如果$\boldsymbol{W}$里的值都比较大，就会发生梯度爆炸，反之则发生梯度消失。

---

参考资料

• https://www.cnblogs.com/pinard/p/6509630.html

• 书籍：《Deep Learning》(深度学习)

---

（欢迎转载，转载请注明出处。欢迎留言或沟通交流： lxwalyw@gmail.com）