分别使用 Python 和 Math.Net 调用优化算法

1. Rosenbrock 函数

在数学最优化中，Rosenbrock 函数是一个用来测试最优化算法性能的非凸函数，由Howard Harry Rosenbrock 在 1960 年提出。也称为 Rosenbrock 山谷或 Rosenbrock 香蕉函数，也简称为香蕉函数。

Rosenbrock 函数的定义如下：

f(x)=100(y−x²)²+(1−x)²

Rosenbrock 函数的每个等高线大致呈抛物线形，其全域最小值也位在抛物线形的山谷中（香蕉型山谷）。很容易找到这个山谷，但由于山谷内的值变化不大，要找到全域的最小值相当困难。

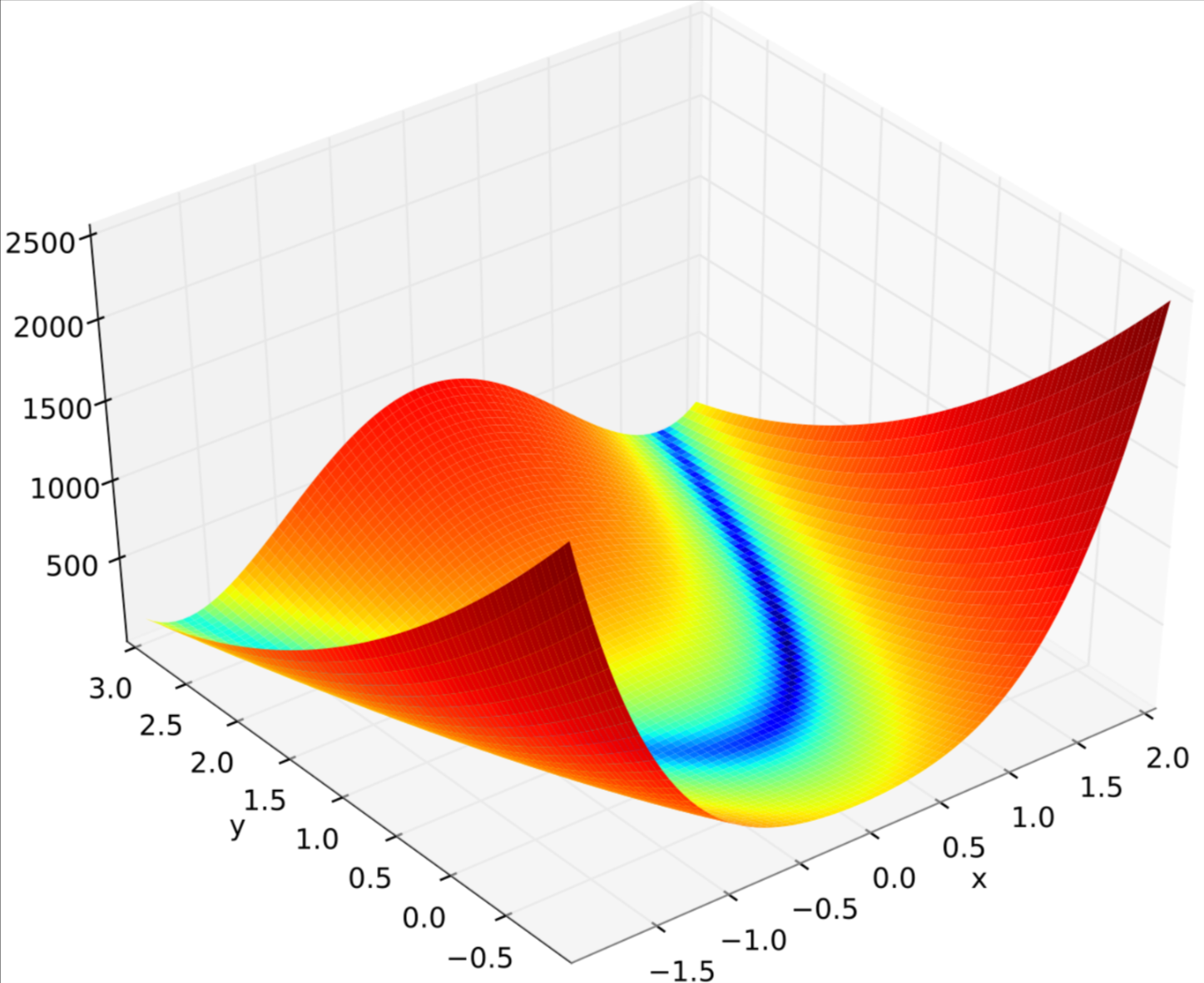
这篇文章分别用 Python 和 Math.Net 求Rosenbrock函数的最小值

2. Python

Python 里面的 scipy.optimize 提供了丰富的优化算法，对于 Rosenbrock函数，它的求解代码如下：

import numpy as np

from scipy.optimize import minimize

def rosenbrock(x):

    return (1 - x[0])**2 + 100 * ((x[1] - x[0] * x[0])**2)

x0 = np.array([1.2, 1.2])

best = minimize(rosenbrock, x0)

print(best)

minimize 有两个参数，其中 rosenbrock 是要去求得最小值得 objective function；x0 是初始值，有时候初始值对结果影响很大。

上面代码得输出如下：

     fun: 3.3496916936926394e-12

hess_inv: array([[0.49944334, 0.99865554],

      [0.99865554, 2.00167338]])

     jac: array([-4.95083209e-05,  2.79682766e-05])

 message: 'Desired error not necessarily achieved due to precision loss.'

    nfev: 159

     nit: 10

    njev: 49

  status: 2

 success: False

       x: array([0.99999874, 0.9999976 ])

即 x(1) 和 y(1) 在接近 (1,1) 的情况下，Rosenbrock 函数有最小值，最小值接近 0。

也可以通过参数 'method='nelder-mead' 指定 minimize 使用 Nelder-Mead 算法，Nelder-Mead 算法是一种求多元函数局部最小值的算法，其优点是不需要函数可导并能较快收敛到局部最小值。使用 Nelder-Mead 算法的输出结果如下：

final_simplex: (array([[0.999993  , 0.99998474],

      [0.99995096, 0.99990431],

      [1.00003347, 1.00007239]]), array([2.05633807e-10, 2.97215547e-09, 4.09754011e-09]))

          fun: 2.0563380675204333e-10

      message: 'Optimization terminated successfully.'

         nfev: 82

          nit: 43

       status: 0

      success: True

            x: array([0.999993  , 0.99998474])

其它参数的说明请参考官方文档。

3. Math.Net

Math.Net 是一个开源项目，旨在构建和维护涵盖基础数学的工具箱，以满足 .Net 开发人员的高级需求和日常需求。其中 Math.NET Numerics 旨在为科学、工程和日常使用中的数值计算提供方法和算法。涵盖的主题包括特殊函数，线性代数，概率模型，随机数，插值，积分变换等等。

要使用 Math.NET Numerics，首先安装它的 Nuget 包：

Install-Package MathNet.Numerics

相比 Python，Math.Net 求解 Rosenbrock 函数的代码复杂些。它先使用 ObjectiveFunction.Value 创建目标函数，然后使用 NelderMeadSimplex 的 FindMinimum 函数求解，代码如下：

using MathNet.Numerics.LinearAlgebra;

using MathNet.Numerics.LinearAlgebra.Double;

using MathNet.Numerics.Optimization;

using System;

double Value(Vector<double> input)

{

    return Math.Pow((1 - input[0]), 2) + 100 * Math.Pow((input[1] - input[0] * input[0]), 2);

}

var obj = ObjectiveFunction.Value(Value);

var solver = new NelderMeadSimplex(convergenceTolerance: 0.0000000001, maximumIterations: 1000);

var initialGuess = new DenseVector(new[] { 1.2, 1.2 });

var result = solver.FindMinimum(obj, initialGuess);

Console.WriteLine("Value:\t" + result.FunctionInfoAtMinimum.Value);

Console.WriteLine("Point:\t" + result.MinimizingPoint[0] + " , " + result.MinimizingPoint[1]);

Console.WriteLine("Iterations:\t" + result.Iterations);

输出如下：

Value:  5.352382362443507E-19

Point:  1.0000000007114838 , 1.0000000014059296

Iterations:     145

虽然 MathNet.Numerics.Optimization 命名空间下还提供了其它类，例如 BfgsBMinimizer 和 NewtonMinimizer，但它们还需要开发者提供梯度函数，这对我来说太复杂了，反而不如 NelderMeadSimplex 好用。

4. 最后

Math.Net 提供了很多多元函数局部最小值的算法，但比起 Python 还是简化了太多，例如我还搞不清楚 Math.Net 中的优化算法怎么添加约束条件，这方面有机会再研究研究。