洛谷 P2783 有机化学之神偶尔会做作弊 解题报告

P2783 有机化学之神偶尔会做作弊

题目背景

XS中学化学竞赛组教练是一个酷爱炉石的人。

有一天他一边搓炉石一边监考，而你作为一个信息竞赛的大神也来凑热闹。

然而你的化竞基友却向你求助了。

“第1354题怎么做”<--手语 他问道。

题目描述

你翻到那一题：给定一个烃，只含有单键（给初中生的一个理解性解释：就是一堆碳用横线连起来，横线都是单条的）。

然后炎魔之王拉格纳罗斯用他的火焰净化了一切环（？？？）。所有的环状碳都变成了一个碳。如图所示。

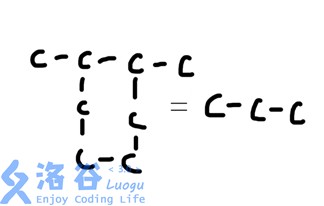
然后指定多组碳，求出它们之间总共有多少碳。如图所示（和上图没有关系）。

但是因为在考试，所以你只能把这个答案用手语告诉你的基友。你决定用二进制来表示最后的答案。如图所示（不要在意，和题目没有什么没关系）。

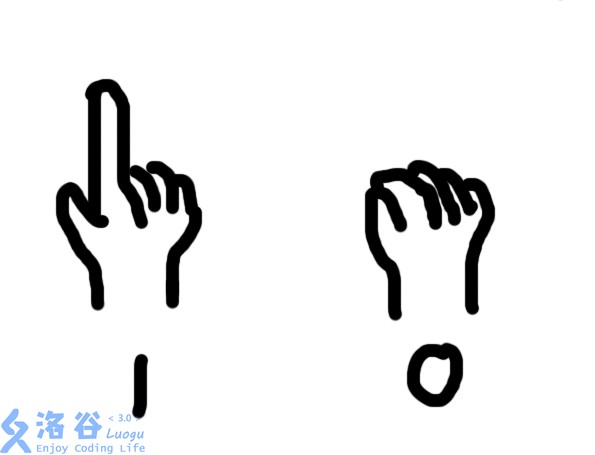
输入输出格式

输入格式：

第一行两个整数\(n,m\).表示有\(n\)个点，\(m\)根键

接下来\(m\)行每行两个整数\(u\)，\(v\)表示\(u\)号碳和\(v\)号碳有一根键

接下来一个整数\(tot\)表示询问次数

接下来\(tot\)行每行两个整数，\(a,b\)表示询问的两个碳的编号

输出格式：

共\(tot\)行

每行一个二进制数

说明

1<n<=10000,1<m<=50000

（两个碳不成环）

---

人生中第一道A掉的黑题！2018.6.9

其实这题思想上不难，简化一下问题即是：对于一个无向图，先把环给缩点缩掉，然后求\(LCA\)即可。

无向图缩点

LCA

---

code:

#include <cstdio>
#include <vector>
#include <cstring>
using namespace std;
const int N=10010;
const int M=50010;
struct Edge
{
    int to,next;
}edge[M<<1],edge1[M<<1];
vector <int > g[N];
int head[N],cnt=0,n,m,head1[N],cnt1=0;
void add(int u,int v)
{
    edge[++cnt].next=head[u];edge[cnt].to=v;head[u]=cnt;
}
void add1(int u,int v)
{
    edge1[++cnt1].next=head1[u];edge1[cnt1].to=v;head1[u]=cnt1;
}
int time=0,dfn[N],low[N],used[N],ha[N],f[N],s[N],ans[N],dis[N],tot=0,n0=0;
void push(int x){s[++tot]=x;}
void pop(){tot--;}
void tarjan(int now,int fa)
{
    dfn[now]=low[now]=++time;
    push(now);
    used[now]=1;
    for(int i=head[now];i;i=edge[i].next)
    {
        int v=edge[i].to;
        if(v!=fa)
        {
            if(!dfn[v])
            {
                tarjan(v,now);
                low[now]=min(low[now],low[v]);
            }
            else if(used[v])
                low[now]=min(low[now],dfn[v]);
        }
    }
    if(low[now]==dfn[now])
    {
        n0++;
        int k;
        do
        {
            k=s[tot];
            ha[k]=n0;
            used[k]=0;
            pop();
        }while(k!=now);
    }
}
int find(int x)
{
    return f[x]=f[x]==x?x:find(f[x]);
}
void merge(int x,int y)
{
    f[find(y)]=find(x);
}
void LCA(int now)//求解lca
{
    used[now]=1;
    for(int i=0;i<g[now].size();i++)
    {
        int v=g[now][i];
        if(!used[v])
        {
            LCA(v);
            merge(now,v);
        }
    }
    for(int i=head1[now];i;i=edge1[i].next)
    {
        int v=edge1[i].to;
        if(used[v])
        {
            int anc=find(v);
            ans[i+1>>1]=dis[v]+dis[now]-(dis[anc]<<1)+1;
        }
    }
}
void out(int x)
{
    int len=0,tt[20];
    while(x)
    {
        tt[++len]=x&1;
        x>>=1;
    }
    for(int i=len;i;i--)
        printf("%d",tt[i]);
    printf("\n");
}
void dfs0(int now,int dep)
{
    used[now]=1;
    dis[now]=dep;
    for(int i=0;i<g[now].size();i++)
    {
        int v=g[now][i];
        if(!used[v]) dfs0(v,dep+1);
    }
}
void init()
{
    for(int i=1;i<=n0;i++) f[i]=i;
    for(int i=1;i<=n0;i++)
        if(!used[i])
            dfs0(i,1);
}
int main()
{
    scanf("%d%d",&n,&m);
    int u,v,q;
    for(int i=1;i<=m;i++)
    {
        scanf("%d%d",&u,&v);
        add(u,v),add(v,u);
    }
    for(int i=1;i<=n;i++)
        if(!dfn[i])
            tarjan(i,0);
    for(int i=1;i<=n;i++)
        for(int j=head[i];j;j=edge[j].next)
        {
            int v=edge[j].to;
            if(ha[v]!=ha[i])
                g[ha[i]].push_back(ha[v]);
        }
    scanf("%d",&q);
    for(int i=1;i<=q;i++)
    {
        scanf("%d%d",&u,&v);
        add1(ha[u],ha[v]);
        add1(ha[v],ha[u]);
    }
    init();
    memset(used,0,sizeof(used));
    for(int i=1;i<=n0;i++)
        if(!used[i])
            LCA(i);
    for(int i=1;i<=q;i++)
        out(ans[i]);
    return 0;
}

---

2018.6.9