Codeforces 1089E - Easy Chess - [DFS+特判][2018-2019 ICPC, NEERC, Northern Eurasia Finals Problem E]

题目链接：https://codeforces.com/contest/1089/problem/E

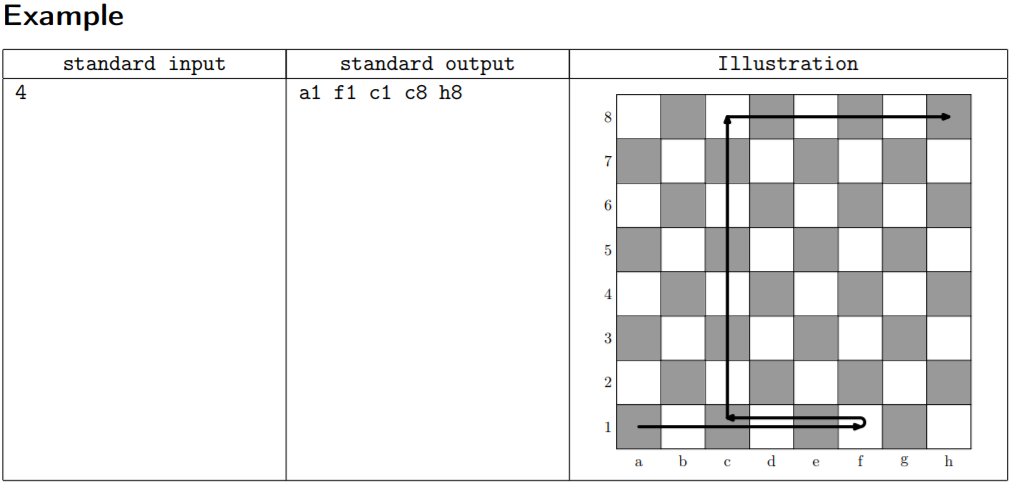
Elma is learning chess figures.

She learned that a rook can move either horizontally or vertically. To enhance her understanding of rook movement Elma’s grandmother gave Elma an 8 × 8 chess board and asked her to find a way to move the rook from a1 to h8 making exactly n moves, so that all visited cells are different.

A visited cell is the initial cell a1 and each cell on which the rook lands after a move.

Input

The input contains a single integer n (2 ≤ n ≤ 63) — the desired number of moves.

Output

Output a space-separated list of n+ 1 visited cells in the order they are visited by the rook.

All cells must be different. The list should start with a1 and end with h8. A solution always exists.

题意：

给你 $8 \times 8$ 的棋盘，有一个棋子车在 $a1$ 位置，现在要经过 $n$ 步移动到达 $h8$ 位置。

要求不能第二次到达曾经到达过的格子，且必须恰好移动 $n$ 步，请给出一种移动方案。

题解：

上来先敲个DFS，万一能过呢？

然后本地跑了一下，发现在 $2 \le n \le 56$ 的范围内跑的飞快，剩下也没几种情况了，干脆特判了之后自己写一个固定走法即可。

AC代码：

#include<bits/stdc++.h>
#define mk(x,y) make_pair(x,y)
using namespace std;
typedef pair<int,int> pii;
int n;
bool vis[][],ok;
vector<pii> ans;
void dfs(int x,int y,int d)
{
    if(ok) return;
    if(d>n) return;
    if(d==n && x== && y==) {ok=;return;}
    for(int i=;i<=;i++)
    {
        if(!vis[i][y])
        {
            ans.push_back(mk(i,y)); vis[i][y]=;
            dfs(i,y,d+);
            if(ok) return;
            ans.pop_back(); vis[i][y]=;
        }
        if(!vis[x][i])
        {
            ans.push_back(mk(x,i)); vis[x][i]=;
            dfs(x,i,d+);
            if(ok) return;
            ans.pop_back(); vis[x][i]=;
        }
    }
}
int main()
{
    while(cin>>n)
    {
        if(n<=)
        {
            ans.clear(); memset(vis,,sizeof(vis));
            ans.push_back(mk(,)); vis[][]=;
            ok=; dfs(,,);
            for(int i=;i<ans.size();i++)
            {
                if(i>) printf(" ");
                printf("%c%d",'a'+ans[i].first-,ans[i].second);
            }
            printf("\n");
        }
        else
        {
            for(int r=;r<=;r++)
            {
                if(r%==) {
                    for(int c=;c>=;c--) printf("%c%d ",'a'+c-,r);
                } else {
                    for(int c=;c<=;c++) printf("%c%d ",'a'+c-,r);
                }
            }
            printf("a7 a8 b8 b7 c7 c8 d8 d7 ");
            switch(n)
            {
            case : printf("h7 h8\n"); break;
            case : printf("e7 h7 h8\n"); break;
            case : printf("e7 f7 h7 h8\n"); break;
            case : printf("e7 f7 g7 h7 h8\n"); break;
            case : printf("e7 e8 f8 f7 h7 h8\n"); break;
            case : printf("e7 e8 f8 f7 g7 h7 h8\n"); break;
            case : printf("e7 e8 f8 f7 h7 g7 g8 h8\n"); break;
            }
        }
    }
}