BZOJ 1179 Atm 题解

BZOJ 1179 Atm 题解

SPFA Algorithm

Tarjan Algorithm

Description

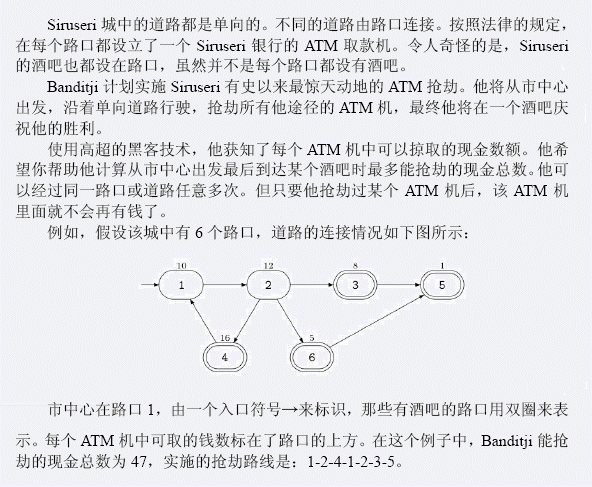
Input

第一行包含两个整数N、M。N表示路口的个数，M表示道路条数。接下来M行，每行两个整数，这两个整数都在1到N之间，第i+1行的两个整数表示第i条道路的起点和终点的路口编号。接下来N行，每行一个整数，按顺序表示每个路口处的ATM机中的钱数。接下来一行包含两个整数S、P，S表示市中心的编号，也就是出发的路口。P表示酒吧数目。接下来的一行中有P个整数，表示P个有酒吧的路口的编号

Output

输出一个整数，表示Banditji从市中心开始到某个酒吧结束所能抢劫的最多的现金总数。

Sample Input

6 7
1 2
2 3
3 5
2 4
4 1
2 6
6 5
10
12
8
16
1 5
1 4
4
3
5
6

Sample Output

47

HINT

50%的输入保证N, M<=3000。所有的输入保证N, M<=500000。每个ATM机中可取的钱数为一个非负整数且不超过4000。输入数据保证你可以从市中心沿着Siruseri的单向的道路到达其中的至少一个酒吧。

————————————————————————————分割线————————————————————————————

思路：

先用Tarjan算法求出途中的所有强连通分量，再讲每个分量值加和为点，再用SPFA算法求出以S为源点，最大价值的路径。

代码如下,(不是我的代码)

 //Code By にしきのまき

 #include<stdio.h>
 #include<algorithm>
 #include<string.h>
 using namespace std;
 struct node
 {
     int v;
     int next;
 };
 int n,m;
 node e[],map[];//邻接表存图
 int st[],head[],cnt;
 int atm[],money[];
 int d[],q[];//最短路径＆SPFA要用的队列
 void build(int a,int b)
 {
     e[++cnt].v=b;
     e[cnt].next=st[a];
     st[a]=cnt;
 }//建图找强连通分量
 int stack[],top;//tarjan需要的栈
 int dfn[],low[],dex;//时间戳（深搜序）、可回溯到的最早栈中时间戳、次序编号
 bool vis[];//tarjan时判断点是否在栈中，SPFA时判断点是否在队列中
 int color[],num;//表示同一强连通分量上的点
 void tarjan(int x)//tarjan找强连通分量
 {
     dfn[x]=++dex;
     low[x]=dex;
     vis[x]=true;
     stack[++top]=x;//当前点入栈
     int i;
     for(i=st[x];i!=;i=e[i].next)//枚举以当前点为起点的边
     {
         int temp=e[i].v;//temp为当前被枚举边的终点
         if(!dfn[temp])//如果当前边终点未被处理
         {
             tarjan(temp);
             low[x]=min(low[x],low[temp]);
         }
         else if(vis[temp])low[x]=min(low[x],dfn[temp]);
     }
     if(dfn[x]==low[x])
     {
         vis[x]=false;
         color[x]=++num;//标记当前强连通分量内的点
         while(stack[top]!=x)//栈顶元素依次出栈
         {
             color[stack[top]]=num;
             vis[stack[top--]]=false;
         }
         top--;
     }
 }
 void add()// 把同一强连通分量上的点缩成一个点，把这些点连成一张新图
 {
     cnt=;
     int i,j;
     for(i=;i<=n;i++)
     {
         for(j=st[i];j!=;j=e[j].next)
         {
             int temp=e[j].v;
             if(color[i]!=color[temp])
             {
                 map[++cnt].v=color[temp];
                 map[cnt].next=head[color[i]];
                    head[color[i]]=cnt;
             }
         }

     }
 }
 void spfa(int x)//SPFA找最长路
 {
     memset(vis,false,sizeof(vis));
     int l=,r=;
     q[l]=x;//初始点放入队列
     vis[x]=true;
     d[x]=money[x];
     while(l<=r)
     {
         int u=q[l++];
         for(int i=head[u];i!=;i=map[i].next)//遍历所有以当前点为起点的边
         {
             int v=map[i].v;
             if(d[v]<d[u]+money[v])
             {
                 d[v]=d[u]+money[v];
                 if(vis[v])continue;
                 q[++r]=v;//如果当前拓展的边的终点不在队列里，就把它放入队尾
                 vis[v]=true;
             }
         }
         vis[u]=false;
     }
 }
 int main()
 {
     int a,b,i,s,p,o,ans=;
     scanf("%d%d",&n,&m);
     for(i=;i<=m;i++)
     {
         scanf("%d%d",&a,&b);
         build(a,b);
     }//建初始图
     for(i=;i<=n;i++)
     {
         if(!dfn[i])tarjan(i);//找强连通分量
     }
     add();//建新图
     for(i=;i<=n;i++)
     {
         scanf("%d",&atm[i]);
         money[color[i]]+=atm[i];
     }
     scanf("%d%d",&s,&p);
     spfa(color[s]);//找单源最短路
     for(i=;i<=p;i++)
     {
         scanf("%d",&o);
         ans=max(ans,d[color[o]]);//找到以酒吧为终点的最长路
     }
     printf("%d",ans);
     return ;
 }

2016-09-14 20:00:54

(完)