EM算法和GMM算法的相关推导及原理
极大似然估计
我们先从极大似然估计说起,来考虑这样的一个问题,在给定的一组样本x1,x2······xn中,已知它们来自于高斯分布N(u, σ),那么我们来试试估计参数u,σ。
首先,对于参数估计的方法主要有矩估计和极大似然估计,我们采用极大似然估计,高斯分布的概率密度函数如下:
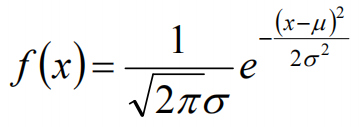
我们可以将x1,x2,······,xn带入上述式子,得:
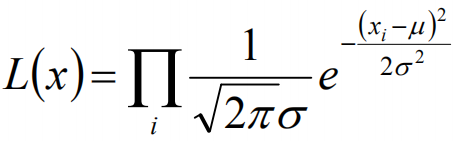
接下来,我们对L(x)两边去对数,得到:
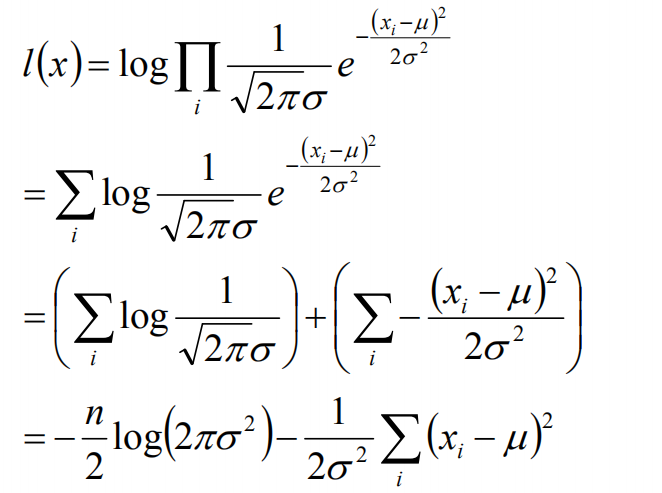
于是,我们得到了l(x)的表达式,下面需要对其计算极大值:
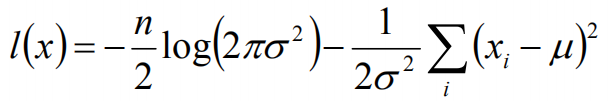
通过对目标函数的参数u,σ分别求偏导,很容易得到:

对于上述的结果,和矩估计是一样,它的含义就是:样本的均值即为高斯分布的均值,样本的方差即为高斯分布的方差。
通过上面的问题分析,我们来看这样的一个问题,假设在班级中随机挑选100名同学,并且测量了这100名同学的身高,如果这100个样本服从的是正态分布,那么我们可以用样本的均值和方差等于正态分布的均值和方差来估计参数u和σ。但是样本中存在男同学和女同学,它们分别服从N1(u1, σ1)和N2(u2, σ2)的分布,那么我们应该如何估计u1, σ1,u2, σ2参数呢?
我们可以通过假设随机变量x是有k个高斯分布混合而成,取各个高斯分布的概率的φ1,φ2,······φk,第i个高斯分布的均值为ui,方差为∑i。那么,我们可以建立如下目标函数:
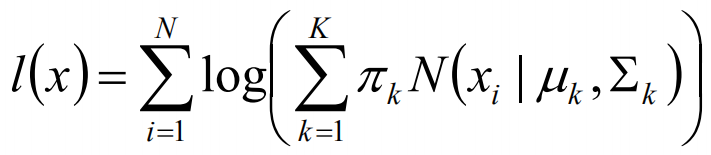
上述的式子中,由于在对数函数中存在加和,无法直接求导计算极大值,我们可以将其分成两步:
第一步:估算数据来自哪个组份
估计数据是有哪个组份生成的概率,对于数据xi来说,它是由第k个组份生成的概率为:
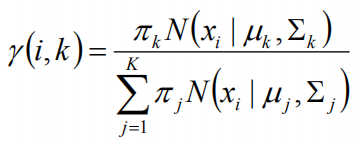
在上面的式子中,u和∑是需要进行估计的,这里采用迭代法,在计算r(i,k)的时候,假定u和∑均为已知的,但是在第一次计算时,我们根据先验知识给定u和∑。
第二步:估计每个组份的参数
假设上一步中得到的r(i,k)就是正确的数据xi由组份k生成的概率,亦可以当做该组份在生成这个数据上所做的贡献,或者也可以看做xi其中r(i,k)*xi部分是由组份k所生成的。对于所有的数据点,现在司机上可以看作组份k生成了{γ(i,k)*xi|i=1,2,…N}这些点。组份k是一个标准的高斯分布,利用上面的结论:
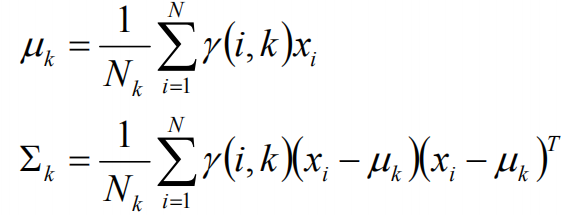
EM算法的提出
假定有训练集{x1, x2,····xm},包含m个独立样本,要求从中找到该组数据的模型p(x, z)的参数。通过构建极大似然估计建立目标函数:
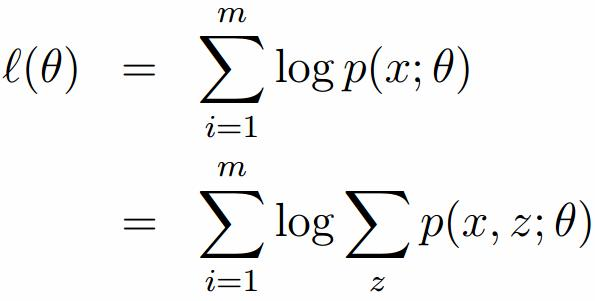
在上面的式子中,z是隐随机变量,直接找到参数的估计是很困难的。这里我们采用建立目标函数的下界,并且求该下界的最大值,不断的重复这个过程,直到收敛到局部的最大值。
Jensen不等式
令Qi是z的某一个分布,并且Qi>=0,有:
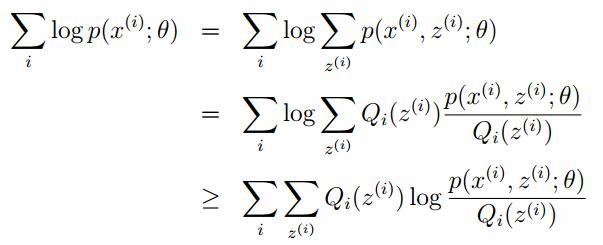
我们需要寻找尽量紧的下界,为了使得等式成立:
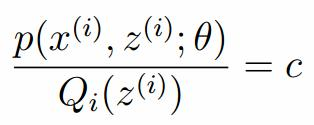
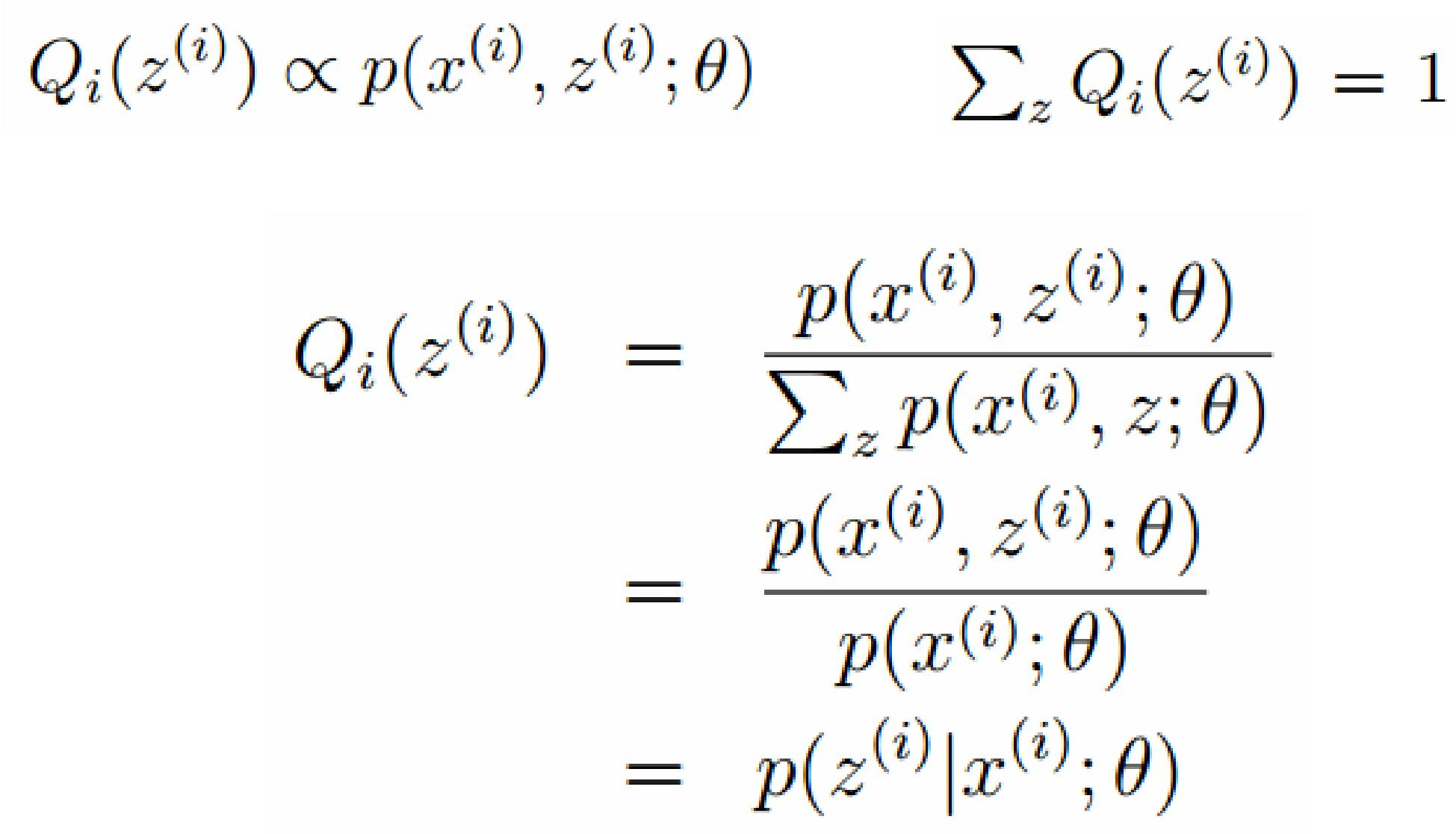
EM算法的整体框架
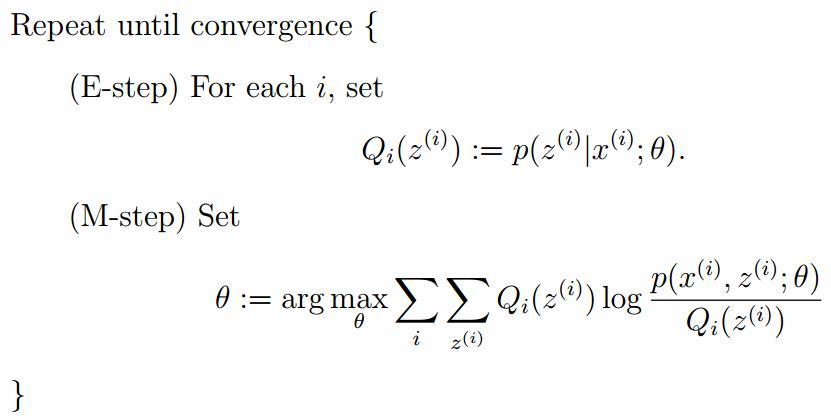
E-step
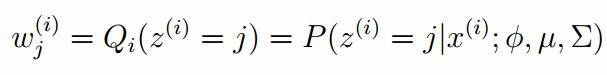
M-step
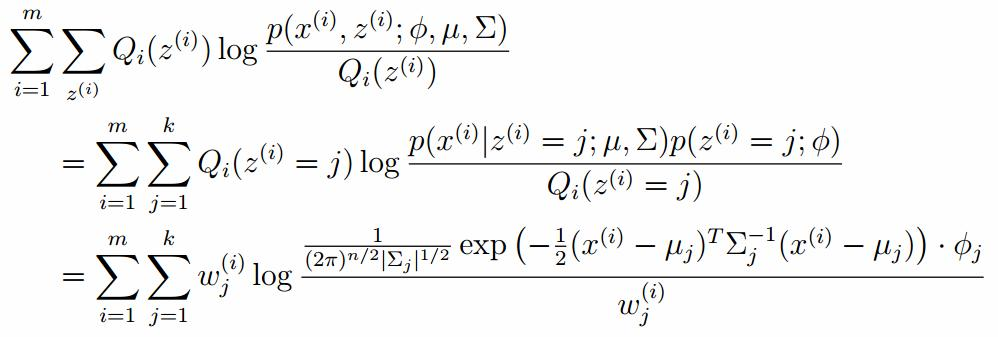
对上面的公式求偏导

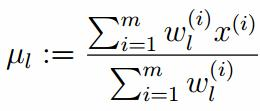
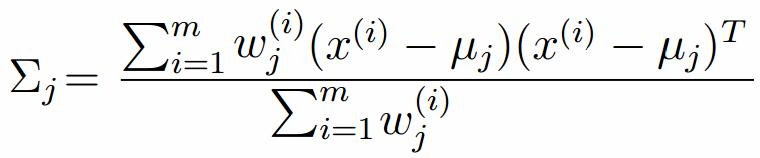
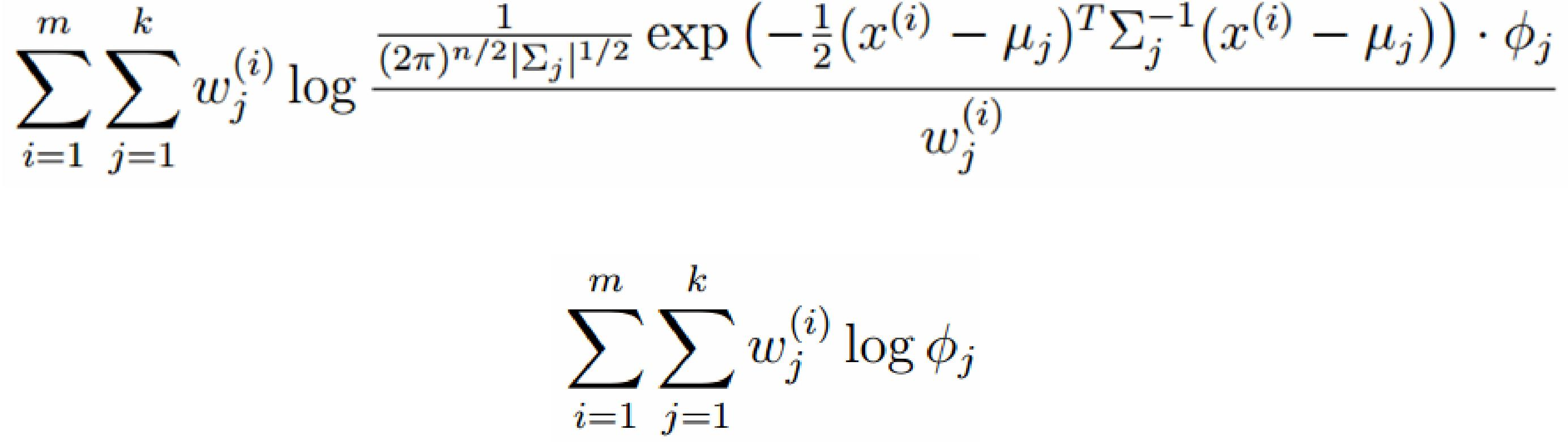
由于多项分布的概率和为1,建立拉个朗日方程:
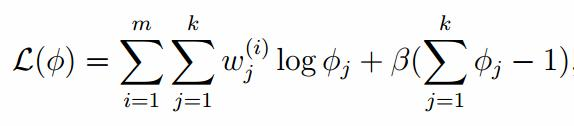
计算偏导:
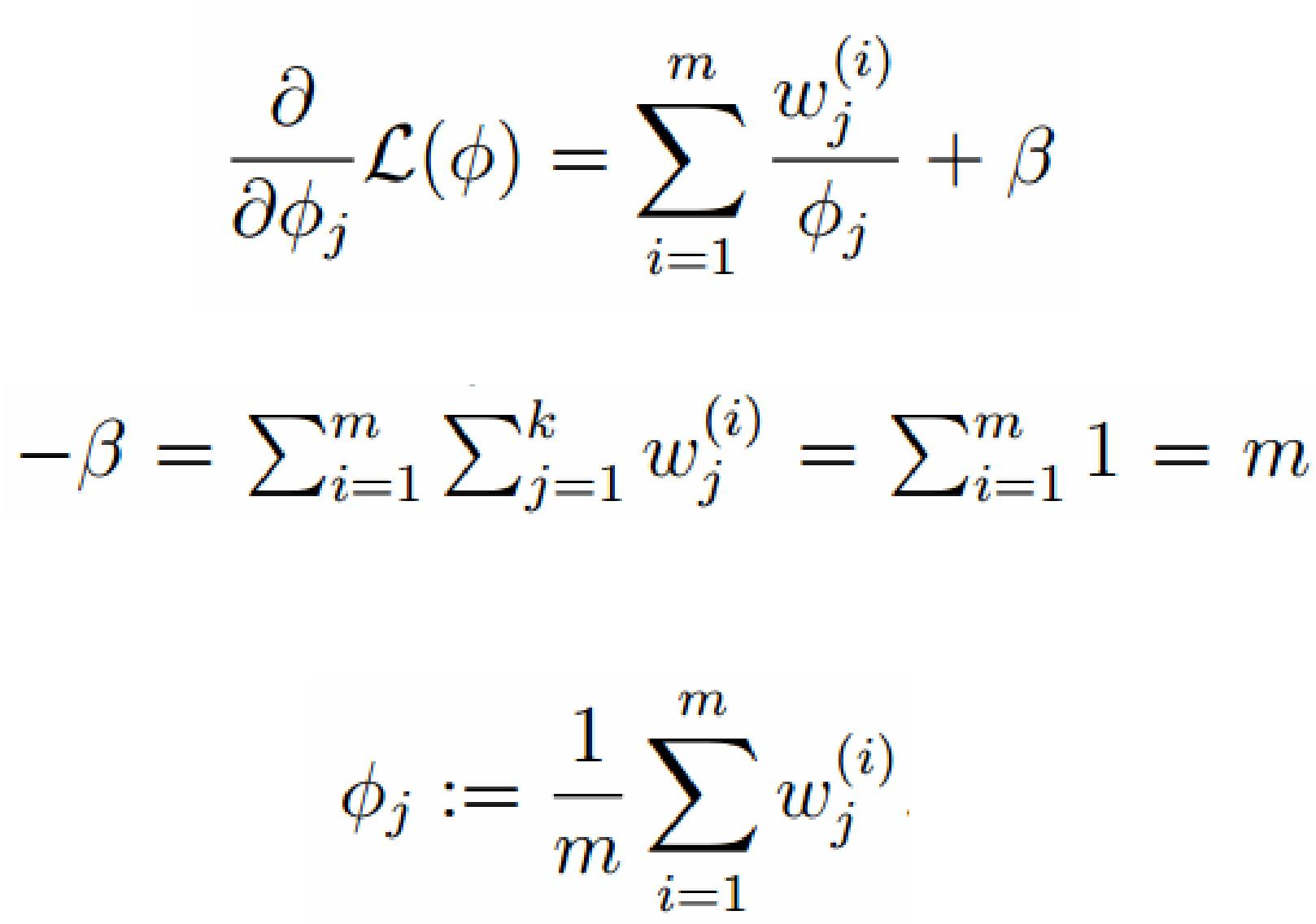
EM算法和GMM算法的相关推导及原理的更多相关文章
- EM算法和GMM模型推导
- IRT模型的参数估计方法(EM算法和MCMC算法)
1.IRT模型概述 IRT(item response theory 项目反映理论)模型.IRT模型用来描述被试者能力和项目特性之间的关系.在现实生活中,由于被试者的能力不能通过可观测的数据进行描述, ...
- 使用Apriori算法和FP-growth算法进行关联分析
系列文章:<机器学习实战>学习笔记 最近看了<机器学习实战>中的第11章(使用Apriori算法进行关联分析)和第12章(使用FP-growth算法来高效发现频繁项集).正如章 ...
- Algorithm --> Kruskal算法和Prim算法
最小生成树之Kruskal算法和Prim算法 Kruskal多用于稀疏图,prim多用于稠密图. 根据图的深度优先遍历和广度优先遍历,可以用最少的边连接所有的顶点,而且不会形成回路.这种连接所有顶点并 ...
- 最短路径——Dijkstra算法和Floyd算法
Dijkstra算法概述 Dijkstra算法是由荷兰计算机科学家狄克斯特拉(Dijkstra)于1959 年提出的,因此又叫狄克斯特拉算法.是从一个顶点到其余各顶点的最短路径算法,解决的是有向图(无 ...
- Prim算法和Kruskal算法的正确性证明
今天学习了Prim算法和Kruskal算法,因为书中只给出了算法的实现,而没有给出关于算法正确性的证明,所以尝试着给出了自己的证明.刚才看了一下<算法>一书中的相关章节,使用了切分定理来证 ...
- 强化学习中REIINFORCE算法和AC算法在算法理论和实际代码设计中的区别
背景就不介绍了,REINFORCE算法和AC算法是强化学习中基于策略这类的基础算法,这两个算法的算法描述(伪代码)参见Sutton的reinforcement introduction(2nd). A ...
- 最小生成树---Prim算法和Kruskal算法
Prim算法 1.概览 普里姆算法(Prim算法),图论中的一种算法,可在加权连通图里搜索最小生成树.意即由此算法搜索到的边子集所构成的树中,不但包括了连通图里的所有顶点(英语:Vertex (gra ...
- mahout中kmeans算法和Canopy算法实现原理
本文讲一下mahout中kmeans算法和Canopy算法实现原理. 一. Kmeans是一个很经典的聚类算法,我想大家都非常熟悉.虽然算法较为简单,在实际应用中却可以有不错的效果:其算法原理也决定了 ...
随机推荐
- pytorch seq2seq模型中加入teacher_forcing机制
在循环内加的teacher forcing机制,这种为目标确定的时候,可以这样加. 目标不确定,需要在循环外加. decoder.py 中的修改 """ 实现解码器 &q ...
- SK-learn实现k近邻算法【准确率随k值的变化】-------莺尾花种类预测
代码详解: from sklearn.datasets import load_iris from sklearn.model_selection import train_test_split fr ...
- 来自BAT大厂前端工程师的自白-怎么才能学好前端
如果说理解学好web前端是先能找到一份工作,那么你应该这样做: 1.制定好一下系统的web前端学习规划,每天定量,学完什么知识点就掌握,能自己应用,而不是能看懂,写不出来东西. 2.不要自己一个人闷头 ...
- 小程序里button边框有黑线解决办法(自定义button样式)
.go_to_user::after{ border:1px solid transparent; } button的class为go_to_user button{ padding:; box-si ...
- Configure Visual Studio with UNIX end of lines
As OP states "File > Advanced Save Options", select Unix Line Endings. https://stackove ...
- 使用react脚手架create-react-app创建react应用
Create React App是一种官方支持的创建单页React应用程序的方法.它提供了一个没有配置的现代构建设置. 一.全局安装脚手架: npm install -g create-react-a ...
- KafkaConsumer assign VS subscribe
背景 在kafka中,正常情况下,同一个group.id下的不同消费者不会消费同样的partition,也即某个partition在任何时刻都只能被具有相同group.id的consumer中的一个消 ...
- 虚拟化VMware之虚拟机备份(1)
之虚拟机备份() 模版:是一种开放,公用.安全的虚拟机压缩格式,通常使用的是扩展名为.ova可以在多个主流虚拟化平台下进行操作 是和 通过技术协作推出的基于磁盘的备份和恢复的新一代解决方案,可靠且易部 ...
- C# richtextbox 自动下拉到最后 方法 & RichTextBox读取txt中文后出现乱码
C# richtextbox 自动滚动到最后 光标到最后 自动显示最后一行 private void richTextBox1_TextChanged(object sender, EventArg ...
- Java——深入理解Java异常体系
该系列博文会告诉你如何从入门到进阶,一步步地学习Java基础知识,并上手进行实战,接着了解每个Java知识点背后的实现原理,更完整地了解整个Java技术体系,形成自己的知识框架. 前言: Java的基 ...
