林轩田机器学习基石笔记2—Learning to Answer Yes/No

机器学习的整个过程：根据模型H，使用演算法A，在训练样本D上进行训练，得到最好的h，其对应的g就是我们最后需要的机器学习的模型函数，一般g接近于目标函数f。本节课将继续深入探讨机器学习问题，介绍感知机Perceptron模型，并推导课程的第一个机器学习算法：Perceptron Learning Algorithm（PLA）。

一、Perceptron Hypothesis Set

某银行要根据用户的年龄、性别、年收入等情况来判断是否给该用户发信用卡。现在有训练样本D，即之前用户的信息和是否发了信用卡。我们要根据D，通过A，在H中选择最好的h，得到g，接近目标函数f。银行用这个模型对以后用户进行判断：发信用卡（+1），不发信用卡（-1）。

在这个机器学习的整个流程中，有一个部分非常重要：就是模型选择，即Hypothesis Set。选择什么样的模型，很大程度上会影响机器学习的效果和表现。下面介绍一个简单常用的Hypothesis Set：感知机（Perceptron）。

我们把用户的个人信息作为特征向量x，令总共有d个特征，每个特征赋予不同的权重w，表示该特征对输出（是否发信用卡）的影响有多大。那所有特征的加权和的值与一个设定的阈值threshold进行比较：大于这个阈值，输出为+1，即发信用卡；小于这个阈值，输出为-1，即不发信用卡。感知机模型，就是当特征加权和与阈值的差大于或等于0，则输出h(x)=1；当特征加权和与阈值的差小于0，则输出h(x)=-1，而我们的目的就是计算出所有权值w和阈值threshold。

为了计算方便，通常我们将阈值threshold当做w0，引入一个x0=1的量与w0相乘，这样就把threshold也转变成了权值w0，简化了计算。h(x)的表达式做如下变换：

我们假设Perceptrons在二维平面上，即h(x)=sign(w0+w1x1+w2x2)。其中，w0+w1x1+w2x2=0是平面上一条分类直线，直线一侧是正类（+1），直线另一侧是负类（-1）。权重w不同，对应于平面上不同的直线。

二、Perceptron Learning Algorithm(PLA)

根据上一部分的介绍，H包含所有可能性的直接（感知器）。接下来，我们的目的就是如何设计一个演算法A，来选择一个最好的直线，能将平面上所有的正类和负类完全分开，也就是找到最好的g，使g≈f。

我们可以使用逐点修正的思想，首先在平面上随意取一条直线，看看哪些点分类错误。然后开始对第一个错误点就行修正，即变换直线的位置，使这个错误点变成分类正确的点。接着，再对第二个、第三个等所有的错误分类点就行直线纠正，直到所有的点都完全分类正确了，就得到了最好的直线。这种“逐步修正”，就是PLA思想所在。

遇到个错误点就进行修正，不断迭代。要注意一点：每次修正直线，可能使之前分类正确的点变成错误点，这是可能发生的。但是没关系，不断迭代，不断修正，最终会将所有点完全正确分类（PLA前提是线性可分的）。这种做法的思想是“知错能改”，有句话形容它：“A fault confessed is half redressed.”

实际操作中，可以一个点一个点地遍历，发现分类错误的点就进行修正，直到所有点全部分类正确。这种被称为Cyclic PLA。

下面用图解的形式来介绍PLA的修正过程：

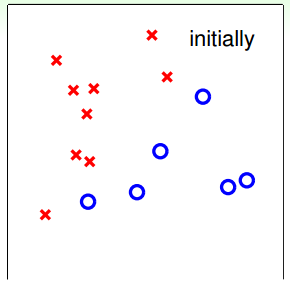
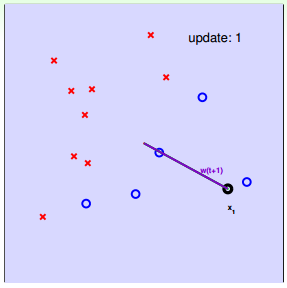
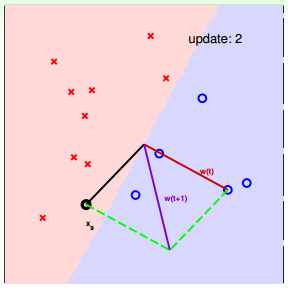
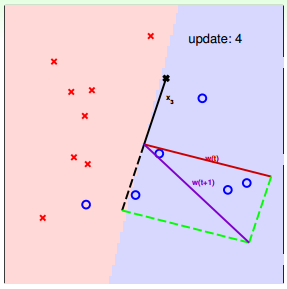
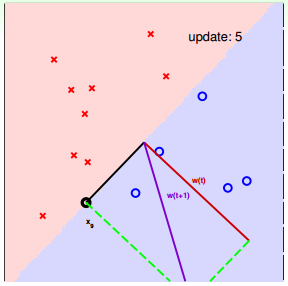
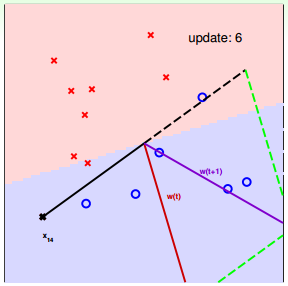
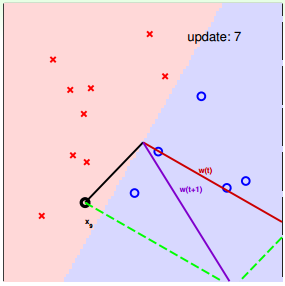
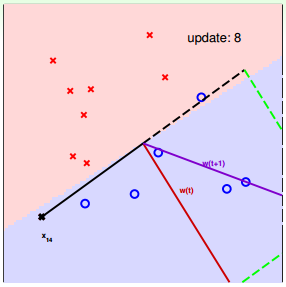
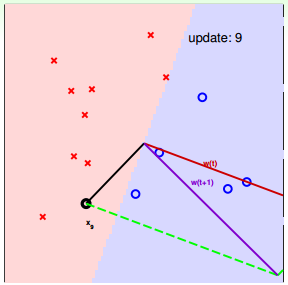
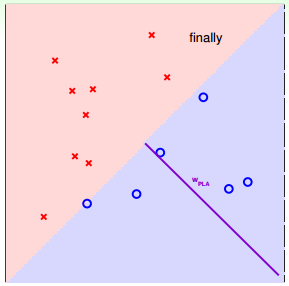
对PLA，有以下两个问题：

PLA迭代一定会停下来吗？如果线性不可分怎么办？
PLA停下来的时候，是否能保证f\approx gf≈g？如果没有停下来，是否有f\approx gf≈g？

三、Guarantee of PLA（可先不看）

根据PLA的定义，当找到一条直线，能将所有平面上的点都分类正确，那么PLA就停止了。要达到这个终止条件，就必须保证D是线性可分（linear separable）。如果是非线性可分的，那么，PLA就不会停止。

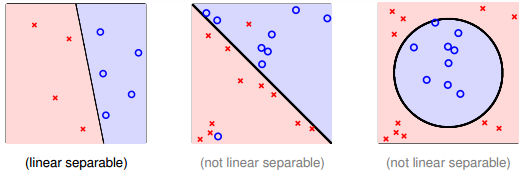
对于线性可分的情况，如果有这样一条直线，能够将正类和负类完全分开，令这时候的目标权重为wf，则对每个点，必然满足yn=sign(wfTxn)，即对任一点：

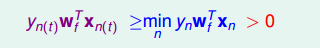
PLA会对每次错误的点进行修正，更新权重wt+1的值，如果wt+1与wf越来越接近，数学运算上就是内积越大，那表示wt+1是在接近目标权重wf，证明PLA是有学习效果的。所以，我们来计算wt+1与wf的内积：

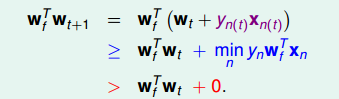
从推导可以看出，wt+1与wf的内积跟wt与wf的内积相比更大了。似乎说明了wt+1更接近wf，但是内积更大，可能是向量长度更大了，不一定是向量间角度更小。所以，下一步，我们还需要证明wt+1与wt向量长度的关系：

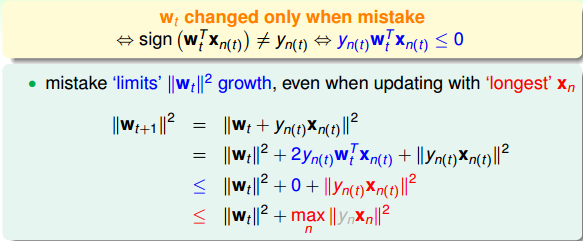
下面贴出来该结论的具体推导过程：

四、Non-Separable Data

上一部分，我们证明了线性可分的情况下，PLA是可以停下来并正确分类的，但对于非线性可分的情况，wf实际上并不存在，那么之前的推导并不成立，PLA不一定会停下来。所以，PLA虽然实现简单，但也有缺点：

对于非线性可分的情况，我们可以把它当成是数据集D中掺杂了一下noise，事实上，大多数情况下我们遇到的D，都或多或少地掺杂了noise。这时，机器学习流程是这样的：

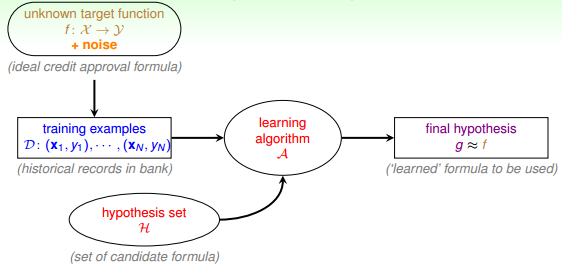
在非线性情况下，我们可以把条件放松，即不苛求每个点都分类正确，而是容忍有错误点，取错误点的个数最少时的权重w：

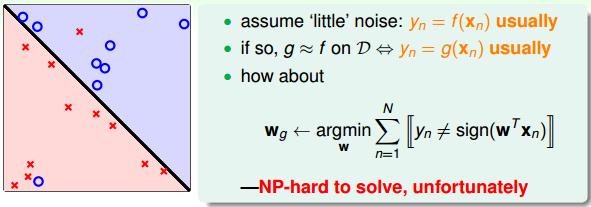
事实证明，上面的解是NP-hard问题，难以求解。然而，我们可以对在线性可分类型中表现很好的PLA做个修改，把它应用到非线性可分类型中，获得近似最好的g。

修改后的PLA称为Packet Algorithm。它的算法流程与PLA基本类似。其原理是：在PLA的基础上，若进行一次调整后发现新的线更好，则抛弃原来线，存储更好线。

如何判断数据集D是不是线性可分？对于二维数据来说，通常还是通过肉眼观察来判断的。一般情况下，Pocket Algorithm要比PLA速度慢一些。

五、总结

本节课主要介绍了线性感知机模型，以及解决这类感知机分类问题的简单算法：PLA。我们详细证明了对于线性可分问题，PLA可以停下来并实现完全正确分类。对于不是线性可分的问题，可以使用PLA的修正算法Pocket Algorithm来解决。