[SDOI2008] 洞穴勘测 (LCT模板)

bzoj 2049 传送门

洛谷P2147 传送门

这个大佬的LCT详解超级棒的！

Link-Cut Tree的基本思路是用splay的森林维护一条条树链。

splay的森林，顾名思义，就是若干splay组成的东西。

每个splay都有一个根节点，所以lct里的splay不能记录根节点，因为根节点有好多。

我们开一个bool数组记录每个点是否为根节点。

每个splay都维护一条重链，重链之间的轻链在splay里只从儿子指向父亲，而父亲并没有这个儿子。

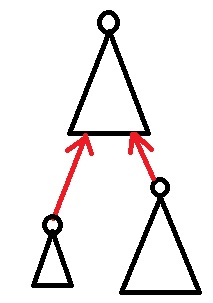
就像图里的红箭头。

每个splay都表示一条重链，这个splay的中序遍历与链上节点的深度顺序是一致的。

接下来是splay里最重要的操作：access(p)

就是指打通从p到整棵树的树根的一条重链。

同时也把p下面接的链变成轻链。

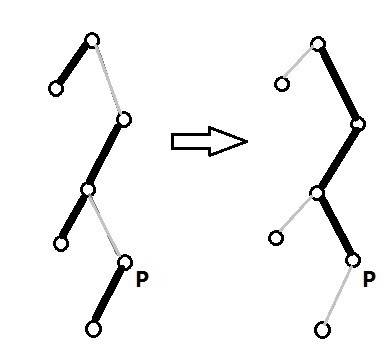
之后还有一个操作：move_to_root，把p变成整棵树的根。

在access之后，p和树根之间是重链直接连接，而一个splay维护一个重链，所以此时p和根已经在一个splay里了。

我们只需要splay(p)即可。

但是这样的话破坏了深度的性质。

把左右反转一下就行了：reverse(p)

接下来就是link和cut的操作。

link(x,y)很简单，mtr(x)，之后接一条从x到y的轻链即可。

cut(x,y)的话，mtr(x)，access(y)，splay(y)，x就是y的左儿子了。删掉父子关系即可。

查询连通性：mtr(x)，access(y)，splay(y)，x就在y的子树里了。x=f[x]一直往上跳，判断最后y的终点是不是x。

这些大概是最最基础的操作了，子树信息什么的都不用维护。

 #include<cstdio>
 #include<cstring>
 #include<algorithm>
 #define id(x) (s[f[x]][1]==x)
 using namespace std;

 int n,m;
 int f[],s[][];
 bool rev[],rt[];

 void reverse(int p)
 {
     swap(s[p][],s[p][]);
     rev[p]^=;
 }

 void pushdown(int p)
 {
     if(!rev[p])return;
     reverse(s[p][]);
     reverse(s[p][]);
     rev[p]=;
 }

 void down(int p)
 {
     if(!rt[p])down(f[p]);
     pushdown(p);
 }

 void rotate(int p)
 {
     int k=id(p);
     int fa=f[p];
     if(rt[fa])rt[p]=,rt[fa]=;
     else s[f[fa]][id(fa)]=p;
     s[fa][k]=s[p][!k];
     s[p][!k]=fa;
     f[p]=f[fa];
     f[fa]=p;
     f[s[fa][k]]=fa;
 }

 void splay(int p)
 {
     down(p);
     while(!rt[p])
     {
         int fa=f[p];
         if(rt[fa])
         {
             rotate(p);
             return;
         }
         if(id(p)^id(fa))rotate(p);
         else rotate(fa);
         rotate(p);
     }
 }

 void access(int p)
 {
     int son=;
     while(p)
     {
         splay(p);
         rt[s[p][]]=,rt[son]=;
         s[p][]=son;
         son=p,p=f[p];
     }
 }

 void mtr(int p)
 {
     access(p);
     splay(p);
     reverse(p);
 }

 void link(int x,int y)
 {
     mtr(x);
     f[x]=y;
 }

 void cut(int x,int y)
 {
     mtr(x);
     access(y);
     splay(y);
     s[y][]=f[x]=;
     rt[x]=;
 }

 void check(int x,int y)
 {
     mtr(x);
     access(y);
     splay(y);
     while(!rt[x])x=f[x];
     printf("%s\n",(x==y?"Yes":"No"));
 }

 int main()
 {
     scanf("%d%d",&n,&m);
     for(int i=;i<=n;i++)rt[i]=;
     char op[];
     int x,y;
     while(m--)
     {
         scanf("%s",op+);
         scanf("%d%d",&x,&y);
         if(op[]=='C')link(x,y);
         if(op[]=='D')cut(x,y);
         if(op[]=='Q')check(x,y);
     }
     return ;
 }