bzoj 1367 - sequence

Description

给定一个序列\(t_1,t_2,\cdots,t_n\)，求一个递增序列\(z_1<z_2<...<z_n\)，

使得 \(R=|t_1−z_1|+|t_2−z_2|+\cdots +|t_n−z_n|\) 的值最小。求\(R\)

Analysis

1.转化

\(z_1<z_2<...<z_n\)的小于号不爽

转化成\(z_1\le z_2\le...\le z_n\)

我们令\(i<j\), 根据条件我们有\(z_j-z_i\ge j-i\)

移一下项则\(z_i-i \le z_j-j\)

我们令\(x_i=t_i-i\)，\(y_i=z_i-i\)

用\(x,y\)相减是等价的, 且转化成了\(y_1\le y_2\le...\le y_n\)

后面我们用\(x,y\)代替\(t,z\)

2.尝试简单化的题目

假如x单调递增，那么\(x_i=y_i\)

假如x单调递减呢，\(y_1=y_2=\cdots=y_n=\)x中位数

注：单调递增可以表示为多个单调递减

证明：

假如有条件\(y_1=y_2=\cdots =y_n\), 这个证明不难

现在稍微加一步

①设\(y_i\)变小，则\(y_1...y_{i-1}\)都变小

若\(i<mid\)，R显然变大

若\(i>mid\)，R变大的点数比变小的点数要多

②设\(y_i\)变大，同理

Solution

对于每个点i一开始属于块i，块中答案\(ans_i=x_i\)

从前往后扫，维护单调队列, 出现y变小的时候退栈

将两个区间合并,合并后区间的ans变为两块一起的中位数

一直合并, 知道上一个区间的y比当前区间的y小

证明:

首先，合并过的区间一定含有至少一个长度大于1的单调减区间

且一开始，合并过的区间里每个区间都只有一个单调减区间

现在我们要证明的就是两个(多个)单调减区间拼在一起的最优答案也是中位数

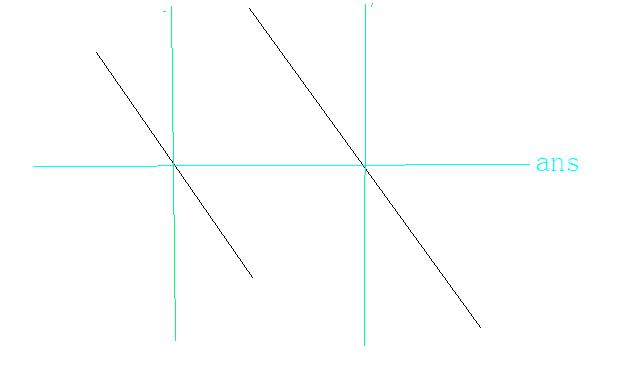
跟前面的证明是类似的，如图(绿线辅助线，黑线表示两个单调减区间)

(考虑移动ans那条线)

正确性

归纳, 初始答案为\(y_1=x_1\)

考虑当前加入\(x_i\)

如果\(y_{i-1}\le x_i\), 显然, 直接令\(y_i = x_i\)是最优的

当出现\(y_{i-1}\gt x_i\)时, 通过合并操作可以使得答案变优, \(y\)最大值变小

Code

#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <cmath>
#include <cctype>
#include <algorithm>
using namespace std;
typedef long long LL;
const int M=1000007;
inline int rd(){
	int x=0;bool f=1;char c=getchar();
	for(;!isdigit(c);c=getchar()) if(c=='-') f=1;
	for(;isdigit(c);c=getchar()) x=x*10+c-48;
	return f?x:-x;
}

int n;
int x[M];
struct node{
	int l,r;
	int rt;
	node(int ll=0,int rr=0,int __=0){
		l=ll;r=rr;
		rt=__;
	}
}que[M];
int tt;

int val[M];
int dist[M];
int sz[M];
int lc[M],rc[M];

int merge(int x,int y){
	if(!x) return y;
	if(!y) return x;
	if(val[x]<val[y]) swap(x,y);
	rc[x]=merge(rc[x],y);
	if(dist[rc[x]]>dist[lc[x]]) swap(lc[x],rc[x]);
	dist[x]=dist[rc[x]]+1;
	sz[x]=sz[lc[x]]+sz[rc[x]]+1;
	return x;//*****
}

void pop(int &x){
	x=merge(lc[x],rc[x]);
}

int main(){
	int i,j;
	n=rd();
	for(i=1;i<=n;i++) x[i]=rd()-i;
	for(i=1;i<=n;i++){
		que[++tt]=node(i,i,i);
		val[i]=x[i];
		dist[i]=sz[i]=1;
		while(tt>1&&val[que[tt].rt]<val[que[tt-1].rt]){
			tt--;
			que[tt].r=que[tt+1].r;
			que[tt].rt=merge(que[tt].rt,que[tt+1].rt);
			while(sz[que[tt].rt]*2>(que[tt].r-que[tt].l+2)){
				pop(que[tt].rt);
			}
		}
	}
	LL ans=0;
	for(i=1;i<=n;i++)
	for(j=que[i].l;j<=que[i].r;j++)
		ans+=abs(val[que[i].rt]-x[j]);
	printf("%lld\n",ans);
	return 0;
}