Baum Welch估计HMM参数实例

Baum Welch估计HMM参数实例

下面的例子来自于《What is the expectation maximization algorithm?》

题面是：假设你有两枚硬币A与B，这两枚硬币抛出正面的概率分别为\(\theta_A\)和\(\theta_B\)。下面给出一些观测的结果，需要你去估计这两个参数\(\theta_A\)与\(\theta_B\)

1. 假设给的数据是完整的数据，也就是样本数据告诉了你，此样本来自硬币A还是硬币B。针对与完整的数据，直接使用极大似然估计即可。具体的计算如下图所示：

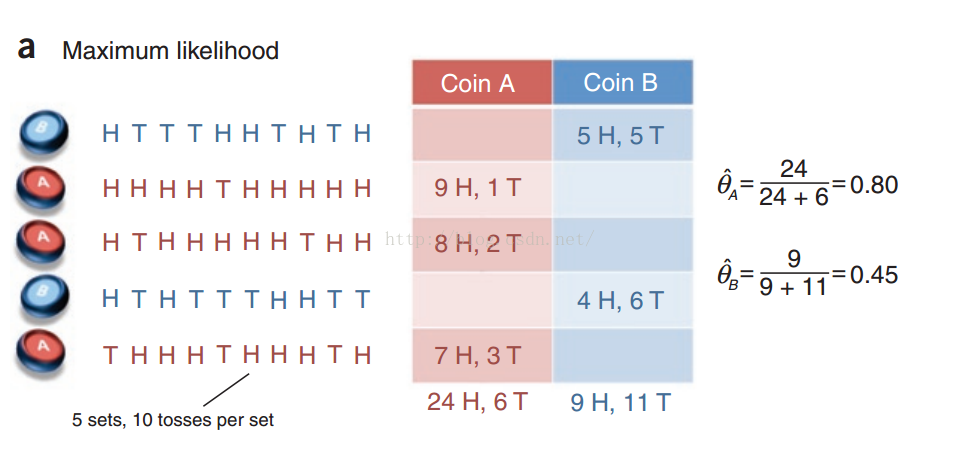
我们可以看到，整个估计的过程就是分别统计来自A的正反面与来自B的正反面，然后内部进行估计（本质上是极大似然）。

1. 如果给的数据是不完整的数据呢，比如我们不知道当前观测序列是来自硬币A 还是硬币B，这个时候，就需要使用EM算法。

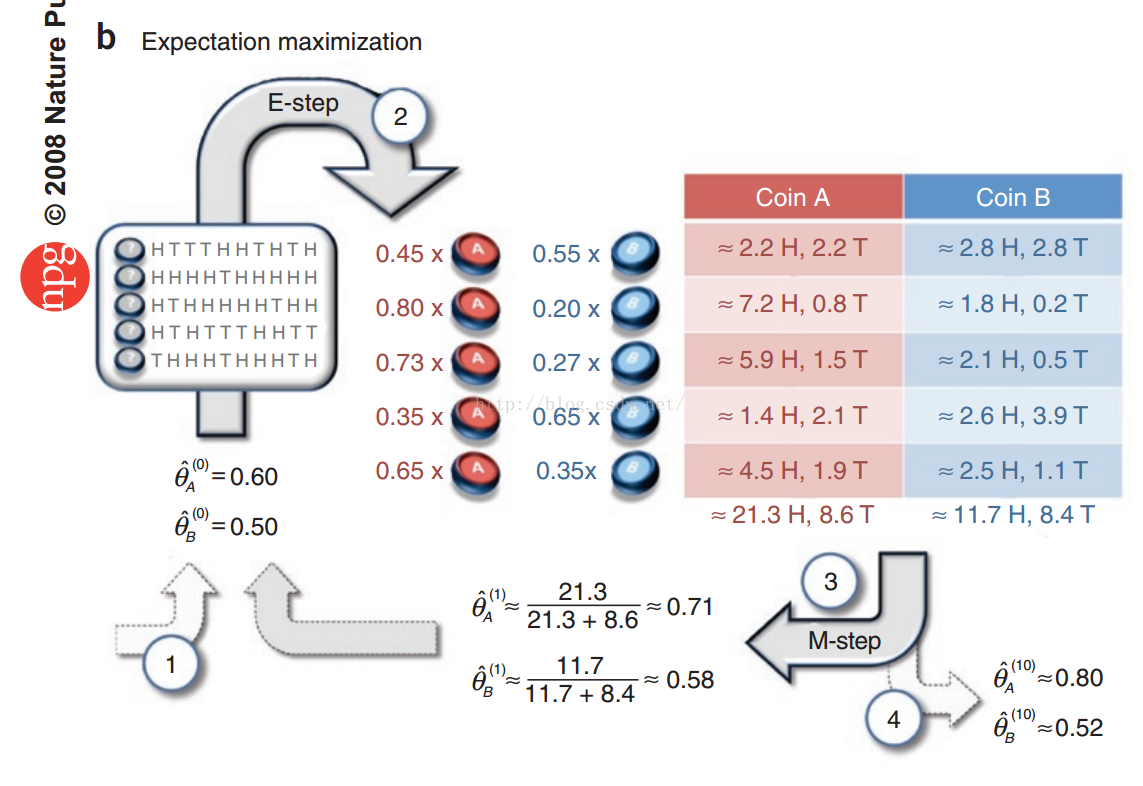
这里解释下求解的过程，首先是我们假设初始的\(\theta_A\)与\(\theta_B\)的值分别为 \(0.6\) 与 \(0.5\). 我们必须要知道当前样本来自A的概率与来自B的概率，然后才能得出来自A的正面期望数和来自B的正面期望数。估计很多人会被卡在这里，我也是。因为不知道图上的\(0.45\)等值是怎么得出来的。 实际上很简单，既然我们有了观测序列，那么我们分别计算一下来自A的似然值，然后再计算一下来自B的似然值。根据似然的大小来决定概率，具体的坐下如下
\[L_A = 0.6^5\times (1 - 0.6)^5 = 0.0007962624\]
然后再计算下来自B的似然值
\[L_B = 0.5^5\times (1 - 0.5)^5 = 0.0009765625\]
然后计算下这两个的比值，来计算来自A的概率
\[P(A) = \dfrac{L_A}{L_A + L_B} = 0.45\]
那么\[P(B) = 1 - P(A) = 0.55\]

然后采用上面求MLE的方法估计参数\(\theta_A\)和参数\(\theta_B\).
重复上述过程几次到收敛即可。