Levenberg-Marquardt

c++ opencv L-M源码

http://www.shenlejun.cn/article/show.asp?id=97

什么是最优化，可分为几大类？

答：Levenberg-Marquardt算法是最优化算法中的一种。最优化是寻找使得函数值最小的参数向量。它的应用领域非常广泛，如：经济学、管理优化、网络分析、最优设计、机械或电子设计等等。
根据求导数的方法，可分为2大类。第一类，若f具有解析函数形式，知道x后求导数速度快。第二类，使用数值差分来求导数。
根据 使用模型不同，分为非约束最优化、约束最优化、最小二乘最优化。
什么是Levenberg-Marquardt算法？
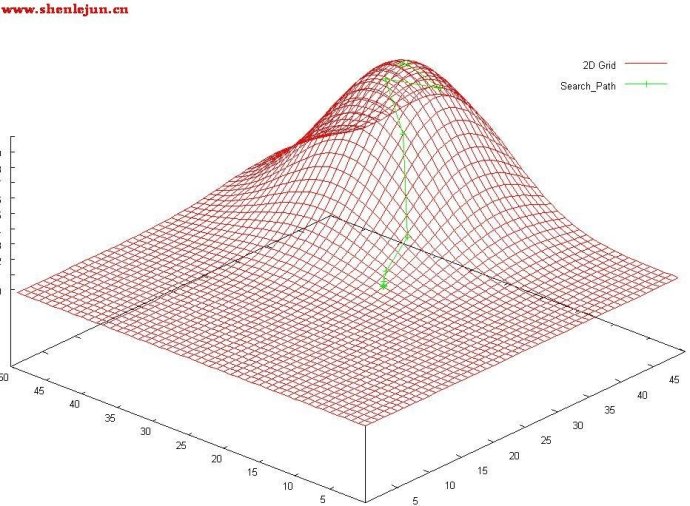
它是使用最广泛的非线性最小二乘算法，中文为列文伯格-马夸尔特法。它是利用梯度求最大（小）值的算法，形象的说，属于“爬山”法的一种。它同时具有梯度法和牛顿法的优点。当λ很小时，步长等于牛顿法步长，当λ很大时，步长约等于梯度下降法的步长。在作者的科研项目中曾经使用过多次。图1显示了算法从起点，根据函数梯度信息，不断爬升直到最高点（最大值）的迭代过程。共进行了12步。（备注：图1中绿色线条为迭代过程）。

图1 LM算法迭代过程形象描述

http://www2.imm.dtu.dk/pubdb/public/publications.php? year=&pubtype=7&pubsubtype=&section=1&cmd=full_view&lastndays=&order=author

或者直接下载pdf原文：
http://www2.imm.dtu.dk/pubdb/views/edoc_download.php/3215/pdf/imm3215.pdf
          
 在LM算法中，每次迭代是寻找一个合适的阻尼因子λ，当λ很小时，算法就变成了GAuss-Newton法的最优步长计算式，λ很大时，蜕化为梯度下降法的最优步长计算式。
Levenberg-Marquardt快速入门教程（荐）
例子程序（MATLAB源程序）
本程序不到100行，实现了求雅克比矩阵的解析解，Levenberg-Marquardt最优化迭代，演示了如何求解拟合问题。采用萧树铁主编的《数学试验》（第二版）（高等教育出版社）中p190例2（血药浓度）来演示。在MATLAB中可直接运行得到最优解。
 
*************************************************************************
% 计算函数f的雅克比矩阵，是解析式
syms a b y x real;
f=a*exp(-b*x);
Jsym=jacobian(f,[a b])
% 拟合用数据。参见《数学试验》，p190，例2
data_1=[0.25 0.5 1 1.5 2 3 4 6 8];
obs_1=[19.21 18.15 15.36 14.10 12.89 9.32 7.45 5.24 3.01];
% 2. LM算法
% 初始猜测s
a0=10; b0=0.5;
y_init = a0*exp(-b0*data_1);
% 数据个数
Ndata=length(obs_1);
% 参数维数
Nparams=2;
% 迭代最大次数
n_iters=50;
% LM算法的阻尼系数初值
lamda=0.01;
% step1: 变量赋值
updateJ=1;
a_est=a0;
b_est=b0;
% step2: 迭代
for it=1:n_iters
    if updateJ==1
        % 根据当前估计值，计算雅克比矩阵
        J=zeros(Ndata,Nparams);
        for i=1:length(data_1)
            J(i,:)=[exp(-b_est*data_1(i)) -a_est*data_1(i)*exp(-b_est*data_1(i))];
        end
        % 根据当前参数，得到函数值
        y_est = a_est*exp(-b_est*data_1);
        % 计算误差
        d=obs_1-y_est;
        % 计算（拟）海塞矩阵
        H=J'*J;
        % 若是第一次迭代，计算误差
        if it==1
            e=dot(d,d);
        end
    end
    % 根据阻尼系数lamda混合得到H矩阵
    H_lm=H+(lamda*eye(Nparams,Nparams));
    % 计算步长dp，并根据步长计算新的可能的\参数估计值
    dp=inv(H_lm)*(J'*d(:));
    g = J'*d(:);
    a_lm=a_est+dp(1);
    b_lm=b_est+dp(2);
    % 计算新的可能估计值对应的y和计算残差e
    y_est_lm = a_lm*exp(-b_lm*data_1);
    d_lm=obs_1-y_est_lm;
    e_lm=dot(d_lm,d_lm);
    % 根据误差，决定如何更新参数和阻尼系数
    if e_lm        lamda=lamda/10;
        a_est=a_lm;
        b_est=b_lm;
        e=e_lm;
        disp(e);
        updateJ=1;
    else
        updateJ=0;
        lamda=lamda*10;
    end
end
%显示优化的结果
a_est
b_est
************************************************************
转自：http://www.shenlejun.cn/my/article/show.asp?id=17&page=2

图1中，算法从山脚开始不断迭代。可以看到，它的寻优速度是比较快的，在山腰部分直接利用梯度大幅度提升（参见后文例子程序中lamda较小时），快到山顶时经过几次尝试（lamda较大时），最后达到顶峰（最大值点），算法终止。

如何快速学习LM算法？

学 习该算法的主要困难是入门难。 要么国内中文教材太艰涩难懂，要么太抽象例子太少。目前，我看到的最好的英文入门教程是K. Madsen等人的《Methods for non-linear least squares problems》本来想把原文翻译一下，贴到这里。请让我偷个懒吧。能找到这里的读者，应该都是E文好手，我翻译得不清不楚，反而事倍功半了。

可在 下面的链接中找到

LM算法是介于牛顿法与梯度下降法之间的一种非线性优化方法，对于过参数化问题不敏感，能有效处理冗余参数问题，使代价函数陷入局部极小值的机会大大减小，这些特性使得LM算法在计算机视觉等领域得到广泛应用。

算法流程

参考文献：

[1]. 张鸿燕， 狄征. Levenberg-Marquardt算法的一种新解释. 计算机工程与应用，2009，45(19),5-8.

from： http://heleiying.blog.163.com/blog/static/3110429201081693815164/