洛谷P4151 [WC2011]最大XOR和路径（线性基）

传送门

不知道线性基是什么东西的可以看看蒟蒻的总结

首先看到异或就想到线性基

我们考虑有一条路径，那么从这条路径走到图中的任意一个环再走回这条路径上，对答案的贡献是这个环的异或和，走到这个环上的路径对答案是没有影响的

以这张（偷来的）图为例

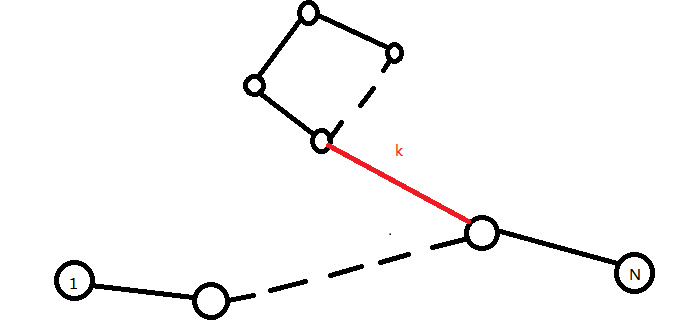
从$1$走到$n$，先走到环再走回来，那么到环上那条路径（红色的）被走了两次，那么异或之后为0，对答案无贡献

那么我们可以随意走一条路径，然后把图上所有环丢到线性基里，求一下在这些线性基下最大能异或和是多少，就是个板子了

那么考虑一下走的路径会不会对答案有影响

依然考虑（盗来的）图

一开始走的是$B$这条路径，但实际上$A$更优，那么$B$路径异或上这整个大环的权值就是$A$路径的权值

找环可以直接dfs

然后没有然后了

 //minamoto
 #include<iostream>
 #include<cstdio>
 #include<cstring>
 #define ll long long
 using namespace std;
 #define getc() (p1==p2&&(p2=(p1=buf)+fread(buf,1,1<<21,stdin),p1==p2)?EOF:*p1++)
 char buf[<<],*p1=buf,*p2=buf;
 inline ll read(){
     #define num ch-'0'
     char ch;bool flag=;ll res;
     while(!isdigit(ch=getc()))
     (ch=='-')&&(flag=true);
     for(res=num;isdigit(ch=getc());res=res*+num);
     (flag)&&(res=-res);
     #undef num
     return res;
 }
 ll b[];
 void insert(ll x){
     for(int i=;i>=;--i){
         if((x>>i)&){
             if(!b[i]){
                 b[i]=x;return;
             }
             x^=b[i];
         }
     }
 }
 ll query(ll x){
     ll res=x;
     for(int i=;i>=;--i)
     if((res^b[i])>res) res^=b[i];
     return res;
 }
 const int N=5e4+,M=2e5+;
 int head[N],Next[M],ver[M],tot;ll edge[M];
 inline void add(int u,int v,ll e){
     ver[++tot]=v,Next[tot]=head[u],head[u]=tot,edge[tot]=e;
 }
 int vis[N];ll del[N];
 void dfs(int u,ll res){
     del[u]=res,vis[u]=;
     for(int i=head[u];i;i=Next[i])
     if(!vis[ver[i]]) dfs(ver[i],res^edge[i]);
     else insert(res^edge[i]^del[ver[i]]);
 }
 int main(){
 //    freopen("testdata.in","r",stdin);
     int n,m,u,v;ll e;n=read(),m=read();
     for(int i=;i<=m;++i)
     u=read(),v=read(),e=read(),add(u,v,e),add(v,u,e);
     dfs(,);
     printf("%lld\n",query(del[n]));
     return ;
 }