Knight Probability in Chessboard

2018-07-14 09:57:59

问题描述：

问题求解：

本题本质上是个挺模板的题目。本质是一个求最后每个落点的数目，用总的数目来除有所可能生成的可能性。这种计数的问题可以使用动态规划来进行解决。

在本题中有两个注意点：

1）可以使用两个数组滚动使用来实现重复利用，这里我的实现使用了一个trick就是结合奇偶性来完成数组滚动；

2）dp数组需要定义成double类型的，如果定义成int类型的，在后期会出现溢出的问题。

    public double knightProbability(int N, int K, int r, int c) {
        double[][][] dp = new double[2][N][N];
        int[][] dir = new int[][]{
                {-1, -2},
                {-2, -1},
                {1, -2},
                {2, -1},
                {-1, 2},
                {-2, 1},
                {1, 2},
                {2, 1},
        };
        dp[0][r][c] = 1;
        for (int k = 0; k < K; k++) {
            fill2D(dp, (k + 1) & 1, N);
            for (int i = 0; i < N; i++) {
                for (int j = 0; j < N; j++) {
                    for (int m = 0; m < 8; m++) {
                        int u = i + dir[m][0];
                        int v = j + dir[m][1];
                        if (u < 0 || u >= N || v < 0 || v >= N) continue;
                        dp[(k + 1) & 1][u][v] += dp[k & 1][i][j];
                    }
                }
            }
        }
        double total = 0;
        for (int i = 0; i < N; i++) {
            for (int j = 0; j < N; j++) {
                total += dp[K & 1][i][j];
            }
        }
        return total / Math.pow(8, K);
    }

    private void fill2D(double[][][] array, int layer, int n) {
        for (int i = 0; i < n; i++) Arrays.fill(array[layer][i], 0);
    }

Follow up：

问题描述：

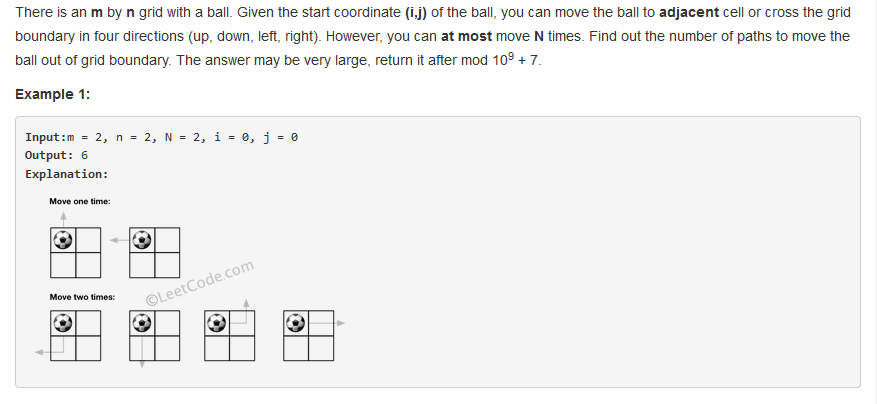
问题求解：

如出一辙。

    public int findPaths(int m, int n, int N, int i, int j) {
        int[][] dp = new int[m][n];
        dp[i][j] = 1;
        int res = 0;
        int mod = (int)Math.pow(10, 9) + 7;
        int[][] dirs = new int[][]{{-1, 0}, {1, 0}, {0, -1}, {0, 1}};
        for (int step = 0; step < N; step++) {
            int[][] cur = new int[m][n];
            for (int pi = 0; pi < m; pi++) {
                for (int pj = 0; pj < n; pj++) {
                    for (int[] dir : dirs) {
                        int x = pi + dir[0];
                        int y = pj + dir[1];
                        if (x < 0 || x >= m || y < 0 || y >= n) {
                            res = (res + dp[pi][pj]) % mod;
                        }
                        else cur[x][y] = (cur[x][y] + dp[pi][pj]) % mod;
                    }
                }
            }
            dp = cur;
        }
        return res;
    }