算法-买卖股票的最佳时机II

01、题目分析

给定一个数组 prices ，它的第 i 个元素 prices[i] 表示一支给定股票第 i 天的价格。你只能选择 某一天 买入这只股票，并选择在 未来的某一个不同的日子 卖出该股票。设计一个算法来计算你所能获取的最大利润。如果你不能获取任何利润，返回 0 。【leetcode】

示例1

输入: [8,9,2,5,4,7,1]
输出: 5

解释：在第3天(股票价格 = 2)的时候买入，在第6天(股票价格 = 7)的时候卖出，最大利润 = 7-2 = 5 ，不能选择在第2天买入，第3天卖出，这样就亏损7了；同时，你也不能在买入前卖出股票。

02、题解分析

方法1

分别计算不同时间买入和卖出的利润，然后不断更新，结束时就能找到利润的最大值

方法2

采用动态规划的方法【参考《团灭 LeetCode 股票买卖问题》】

对于动态规划方法，我们具体到每一天，看看总共有几种可能的「状态」，再找出每个「状态」对应的「选择」。我们要穷举所有「状态」，穷举的目的是根据对应的「选择」更新状态。

dp[i][0] = max(dp[i-1][0], dp[i-1][1] + prices[i]);
解释：今天我没有股票，有两种可能：
      要么是我昨天就没有，然后今天选择无操作，所以我今天还是没有持有      【dp[i-1][0]】
      要么是我昨天持有股票，但是今天我卖出了，所以我今天没有持有股票了    【dp[i-1][1] + prices[i]】
dp[i][1] = max(dp[i-1][1], -prices[i]);
解释：今天我持有股票，有两种可能：
      要么我昨天就持有着股票，然后今天选择无操作，所以我今天还持有着股票  【dp[i-1][1]】
      要么我昨天本没有持有，今天买入股票                               【-prices[i]】

由递推公式 dp[i][0] = max(dp[i - 1][0], -prices[i]); 和 dp[i][1] = max(dp[i - 1][1], prices[i] + dp[i - 1][0]);可以看出其基础都是要从dp[0][0]和dp[0][1]推导出来。

那么dp[0][0]表示第0天没有股票，不持有股票那么现金就是0，所以dp[0][0] = 0;

dp[0][1]表示第0天不持有股票，此时的持有股票就一定是买入股票了，因为不可能有前一天推出来，所以dp[0][0] -= prices[0];

方法3

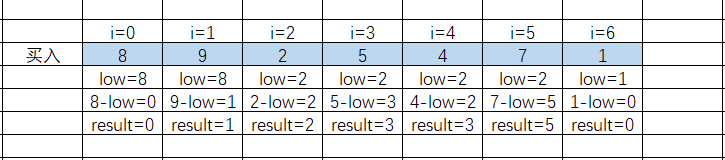
因为股票就买卖一次，那么贪心的想法很自然就是取最左最小值，然后依次用右边的值减去最小值，然后更新结果【参考代码随想录】

03、题解

方法1

// 方法1
int maxProfit(int prices[],int len)
{
  if (len < 2) {
    return 0 ;
  }

  int ans=0;
  for(int i=0; i<len; i++) {
    for(int j=i+1; j<len; j++) {
      ans = max(ans, prices[j] - prices[i]);
    }
  }
  return max(0, ans);
}

方法2

// 方法2
int maxProfit5(int prices[],int len)
{
  if (len < 2) {
    return 0 ;
  }

  int dp[len][2]= {0};
  dp[0][0]=0;
  dp[0][1]=-prices[0];

  for (int i = 1; i < len; i++) {
    dp[i][0] = max(dp[i-1][0], dp[i-1][1] + prices[i]);
    dp[i][1] = max(dp[i-1][1], -prices[i]);
  }
  return dp[len - 1][0];
}

方法3

//方法3
int maxProfit5(int prices[],int len)
{
  if (len < 2) {
    return 0 ;
  }

  int low = 10000;
  int result = 0;
  for (int i = 0; i < len; i++) {
    low = min(low, prices[i]);  		// 更新左边最小价格
    result = max(result, prices[i] - low); 	// 更新最大区间利润
  }
  return result;
}

04、测试结果

  int len = 7;
  int prices[len]= {8,9,2,5,4,7,1};