[Leetcode 787]中转K站内最便宜机票
题目
n个城市,想求从src到dist的最廉价机票
有中转站数K的限制,即如果k=5,中转10次机票1000,中转5次机票2000,最后返回2000
There are n cities connected by some number of flights. You are given an array flights where flights[i] = [fromi, toi, pricei] indicates that there is a flight from city fromi to city toi with cost pricei.
You are also given three integers src, dst, and k, return the cheapest price from src to dst with at most k stops. If there is no such route, return -1.
Example 1:

Input: n = 3, flights = [[0,1,100],[1,2,100],[0,2,500]], src = 0, dst = 2, k = 1
Output: 200
Explanation: The graph is shown.
The cheapest price from city0to city2with at most 1 stop costs 200, as marked red in the picture.
Example 2:

Input: n = 3, flights = [[0,1,100],[1,2,100],[0,2,500]], src = 0, dst = 2, k = 0
Output: 500
Explanation: The graph is shown.
The cheapest price from city0to city2with at most 0 stop costs 500, as marked blue in the picture.
Constraints:
1 <= n <= 1000 <= flights.length <= (n * (n - 1) / 2)flights[i].length == 30 <= fromi, toi < nfromi != toi1 <= pricei <= 104- There will not be any multiple flights between two cities.
0 <= src, dst, k < nsrc != dst
思路
和https://www.cnblogs.com/inku/p/15622556.html类似
这题多了一个stepCheck,check中转的次数
dijsktra+优先队列
代码
class Solution {
public int findCheapestPrice(int n, int[][] flights, int src, int dst, int k) {
int[][] adj=new int[n][n];
for(int[] flight_line:flights){
//flighr_line: {from,to,money}
adj[flight_line[0]][flight_line[1]]=flight_line[2];
}
int[] cost=new int[n];
int[] stepCheck=new int[n];
Arrays.fill(cost,Integer.MAX_VALUE);
Arrays.fill(stepCheck,Integer.MAX_VALUE);
cost[src] = 0;
stepCheck[src] = 0;
//int[] cur position,cost,stops
PriorityQueue<int[]> pq=new PriorityQueue<>(new Comparator<int[]>() {
@Override
public int compare(int[] o1, int[] o2) {
return o1[1]-o2[1];
}
});
//pq.add(new int[]{0,0,1}); 错误!
pq.offer(new int[]{src, 0, 0});//起点不一定是0,本身不算中转
while (!pq.isEmpty()){
int[] curPos=pq.poll();
int curNode=curPos[0];
int curCost=curPos[1];
int curStop=curPos[2];
if(curNode==dst)
return curCost;
if(curStop==k+1)
continue;
for(int i=0;i<n;i++){
//两地有机票
if(adj[curNode][i]>0){
int cost_try=adj[curNode][i]+curCost;
if(cost_try<cost[i]){
cost[i]=cost_try;
pq.offer(new int[]{i,cost_try,curStop+1});//便宜的情况,加入
}
else if(curStop<stepCheck[i]){
pq.offer(new int[]{i,cost_try,curStop+1});//没便宜,但站数更少的情况,也加入
}
stepCheck[i]=curStop;//本身不算stop
}
}
}
return cost[dst]==Integer.MAX_VALUE?-1:cost[dst];
}
}
疑问
else if(curStop<stepCheck[i]){
pq.offer(new int[]{i,cost_try,curStop+1});//没便宜,但站数更少的情况,也加入
}
没便宜(cost更多),但站数更少的情况下虽然加入了,但因优先队列是按cost排序,那岂不是永远取不到?它的意义?
A:取得到,先加进去再说。虽然当前cost多,但后面的cost可能极小,成为最终解的一部分
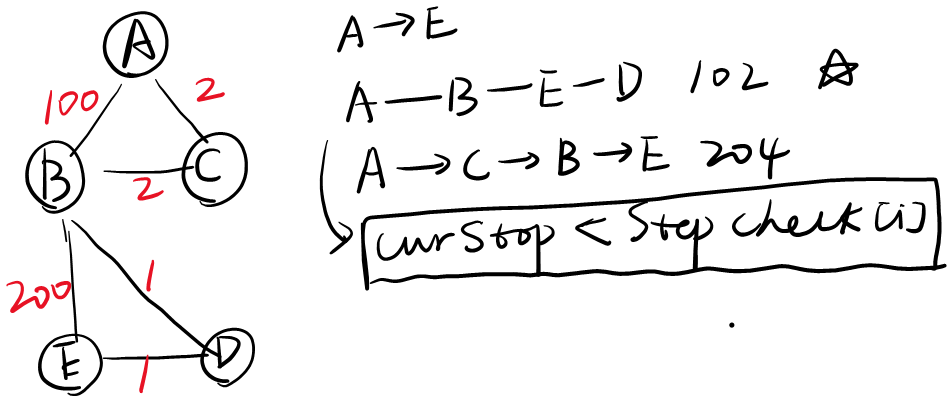
[Leetcode 787]中转K站内最便宜机票的更多相关文章
- LeetCode——787. K 站中转内最便宜的航班
有 n 个城市通过 m 个航班连接.每个航班都从城市 u 开始,以价格 w 抵达 v. 现在给定所有的城市和航班,以及出发城市 src 和目的地 dst,你的任务是找到从 src 到 dst 最多经过 ...
- Java实现 LeetCode 787 K 站中转内最便宜的航班(两种DP)
787. K 站中转内最便宜的航班 有 n 个城市通过 m 个航班连接.每个航班都从城市 u 开始,以价格 w 抵达 v. 现在给定所有的城市和航班,以及出发城市 src 和目的地 dst,你的任务是 ...
- 【力扣leetcode】-787. K站中转内最便宜的航班
题目描述: 有 n 个城市通过一些航班连接.给你一个数组 flights ,其中 flights[i] = [fromi, toi, pricei] ,表示该航班都从城市 fromi 开始,以价格 p ...
- leetcode 787. K 站中转内最便宜的航班
问题描述 有 n 个城市通过 m 个航班连接.每个航班都从城市 u 开始,以价格 w 抵达 v. 现在给定所有的城市和航班,以及出发城市 src 和目的地 dst,你的任务是找到从 src 到 dst ...
- 【力扣】787. K 站中转内最便宜的航班加权——有向图最短路径
前言 我感觉这题比较有代表性,所以记录一下,这题是加权有向图中求最短路径的问题. 题目 787. K 站中转内最便宜的航班 动态规划 假设有一条路径是[src, i, ..., j, dst],解法一 ...
- [Swift]LeetCode787. K 站中转内最便宜的航班 | Cheapest Flights Within K Stops
There are n cities connected by m flights. Each fight starts from city u and arrives at v with a pri ...
- leetcode_787【K 站中转内最便宜的航班】
有 n 个城市通过 m 个航班连接.每个航班都从城市 u 开始,以价格 w 抵达 v. 现在给定所有的城市和航班,以及出发城市 src 和目的地 dst,你的任务是找到从 src 到 dst 最多经过 ...
- Lucene.net站内搜索—4、搜索引擎第一版技术储备(简单介绍Log4Net、生产者消费者模式)
目录 Lucene.net站内搜索—1.SEO优化 Lucene.net站内搜索—2.Lucene.Net简介和分词Lucene.net站内搜索—3.最简单搜索引擎代码Lucene.net站内搜索—4 ...
- Lucene.net站内搜索—1、SEO优化
目录 Lucene.net站内搜索—1.SEO优化 Lucene.net站内搜索—2.Lucene.Net简介和分词Lucene.net站内搜索—3.最简单搜索引擎代码Lucene.net站内搜索—4 ...
- 1.PHP站内搜索 分类: PHP开发实例 2015-07-31 22:48 4人阅读 评论(0) 收藏
PHP站内搜索:多关键字.加亮显示 1.SQL语句中的模糊查找 $sql = "SELECT * FROM `message` WHERE `content`like '%$k[0]%' a ...
随机推荐
- 华为交换机,改vlan的方法
telnet 登录1.1.1.111, 如果登录再到其他交换机,需要在用户状态,telnet其他的ip.不能在系统用户状态下跳转登录. sys改为系统用户 状态符由尖括号,改为方括号 display ...
- https原理(四)双向实践(java客户端+tcp代理)
本文采用客户端与服务端共用一个密钥对 1 将https代理服务器(三)实践中的mkcert p12分解为一个公钥一个私钥 mac@macdeMacBook mkcert % openssl pkcs1 ...
- https原理(三)双向实践(curl)
接 https代理服务器(三)实践,实践双向ssl 本文采用客户端与服务端不同密钥对 1 mkcert myclient 生成客户端公钥 私钥 2 mkcert -pkcs12 myclient 也可 ...
- python IDLE清除窗口内容和new file里代码加行业的操作
这个其实比较简单,主要是从网上下载好ClearWindow.py这个文件,然后把文件放到./Lib/idlelib下面,同时打开该文件夹下config-extensions.def文件,在文件尾加入下 ...
- Python学习笔记组织文件之用zipfile模块压缩文件
随笔记录方便自己和同路人查阅. #------------------------------------------------我是可耻的分割线--------------------------- ...
- dp泄露
DP泄露 选了三道与RSA的dp泄露有关的题,dp泄露算是比较有辨识度的题型. 目录 DP泄露 原理 ctfshow funnyrsa3 分析 解答 BUUCTF RSA2 分析 解答 [羊城杯 20 ...
- HTML-background-image
background-image:用于设置需要显示背景图片: 例如-->background-image:url(demo.jpg); 大家知道ulr()中是填写路径:(现在假设背景图片名字叫做 ...
- 打卡node day01--基础和fs内置模块
一, 检查 node 版本 node -v 或 node --version 二,检查安装过的node 版本(nvm node 版本管理工具 安装链接 参考百度) nvm ls 三,切换node 版 ...
- ORACLE查看会话的大小及终止会话
一.出现PGA不足时,我们可以查看用户会话大小,结束相应会话 方法一 Select Server, Osuser, Name, Value / 1024 / 1024 Mb, s.Sql_Id, Sp ...
- from pathlib import Path
from pathlib import Path #引入库 P.parent #获取父级目录 P.exists() #判断当前路径是否存在 P.mkdir(parents=Fasle) # 根据路径创 ...
