Java 求解自幂数(水仙花数)

什么是自幂数

如果在一个固定的进制中，一个 n 位自然数等于自身各个数位上数字的 n 次幂之和，则称此数为自幂数。

例如：在十进制中，153 是一个三位数，各个数位的3次幂之和为

1^3+5^3+3^3=153，所以 153 是十进制中的自幂数。

在n进制中，所有小于n的正整数都为自幂数，比如2进制中1是自幂数，3 进制中

1 和 2 都是自幂数，4 进制中 1，2 和 3 都是自幂数......

Java pow() 方法扩展

pow() 方法用于返回第一个参数的第二个参数次方。

语法

double pow(double base, double exponent)

参数

base -- 任何原生数据类型。

exponent -- 任何原生数据类型。

返回值

返回第一个参数的第二个参数次方。

实例：

public class Test{
    public static void main(String args[]){
        double x = 11.635;
        double y = 2.76;

        System.out.printf("e 的值为 %.4f%n", Math.E);
        System.out.printf("pow(%.3f, %.3f) 为 %.3f%n", x, y, Math.pow(x, y));
    }
}

输出结果为：

e 的值为 2.7183
pow(11.635, 2.760) 为 874.008

---

如何求自幂数

代码如下：

package com.exercise.demo3;

public class Test1 {
    public static void main(String[] args) {

        System.out.println("范围内的自幂数有：");
        //自幂数查找的范围
        for (int i = 0; i <= 1000; i++) {
            //判断i是否为水仙花数(自幂数)
            int n = 1, temp = i, sum = 0;
            /*计算i是几位数(n表示i为一个n位数)
            这里将i赋值给临时遍历temp防止下面i的值被改变*/
            while ((temp /= 10) != 0) {
                //只要结果不为0，temp每除以10，n加1从而可得到i的位数
                n++;
            }
            //与上相同
            temp = i;
            //计算i的每一位的n次方之和sum
            while (temp != 0) {
                /*先取余后除10，依次计算出i的个位数、十位数、百位数
                利用pow函数求各个位的三次方然后通过sum将值累加*/
                sum += Math.pow(temp % 10, n);
                temp /= 10;
            }
            //比较i == sum，得到范围内所有自幂数并打印
            if (i == sum) {
                System.out.print(i + " ");
            }
        }
    }
}

如图：

---

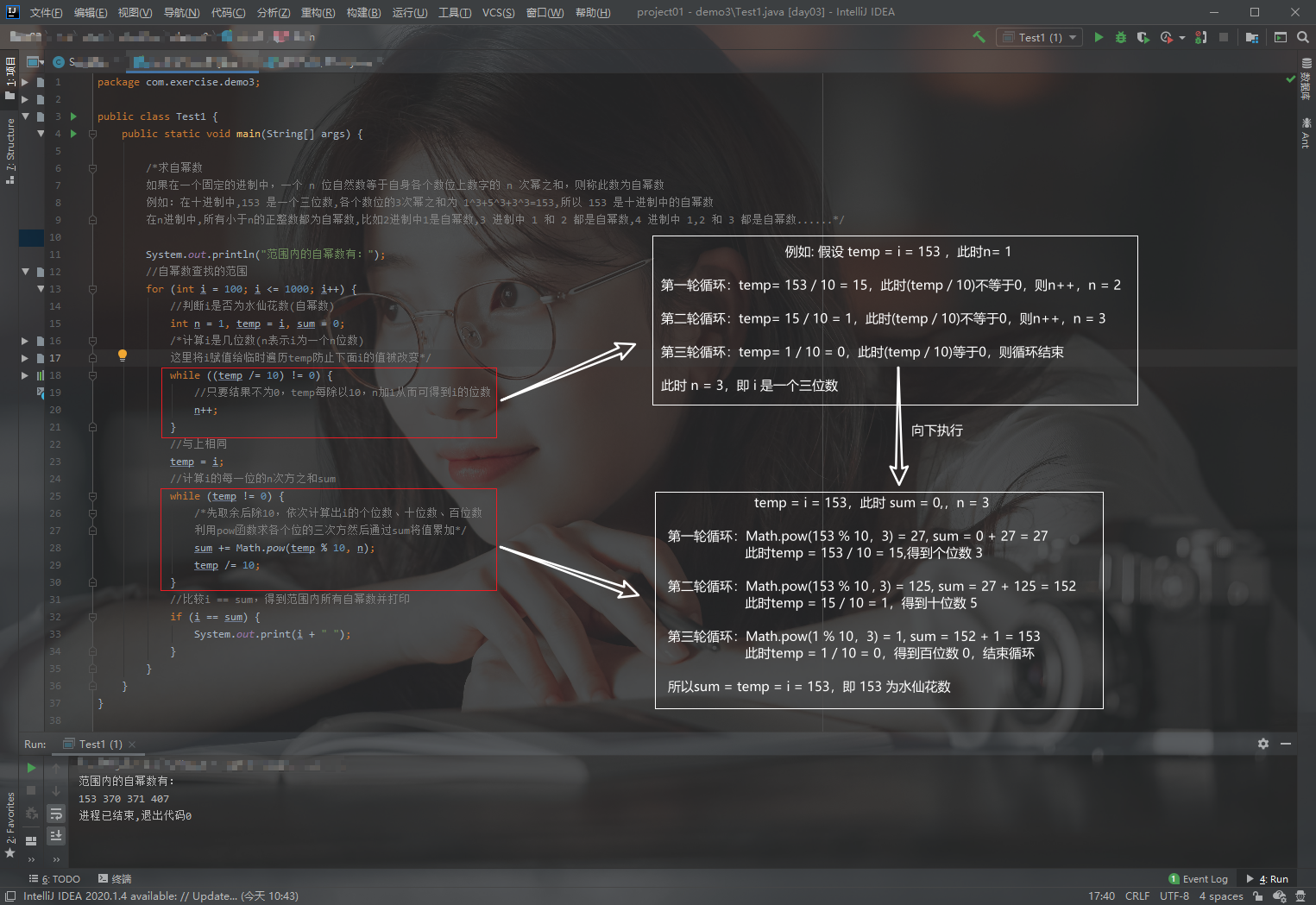
什么是水仙花数

“水仙花数”也被称为：超完全数字不变数、自恋数、自幂数、阿姆斯壮数 或 阿姆斯特朗数

水仙花数是指一个 3 位数，它的每个位上的数字的 3 次幂之和等于它本身。

例如：1^3 + 5^3+ 3^3 = 153。

水仙花数只是自幂数的一种，严格来说 3 位数的 3 次幂数才称为水仙花数。

---

如何求水仙花数

代码如下：

package com.exercise.demo01;

public class Test03 {
    public static void main(String[] args) {

        int count = 0;
        System.out.print("水仙花数有：");
        //遍历指定范围内所有的数值
        for (int i = 100; i < 1000; i++) {
            //算出个位
            int a = i % 10;
            //算出十位
            int b = i / 10 % 10;
            //算出百位
            int c = i / 100;
            //判断每个位上的立方和是否等于i
            if ((a * a * a + b * b * b + c * c * c) == i) {
                //输出水仙花数
                System.out.print(i + " ");
                //计算个数加1
                count++;
            }
        }
        System.out.println();
        System.out.println("--------------------------");
        System.out.println("水仙花数的个数为：" + count);
    }
}

如图：

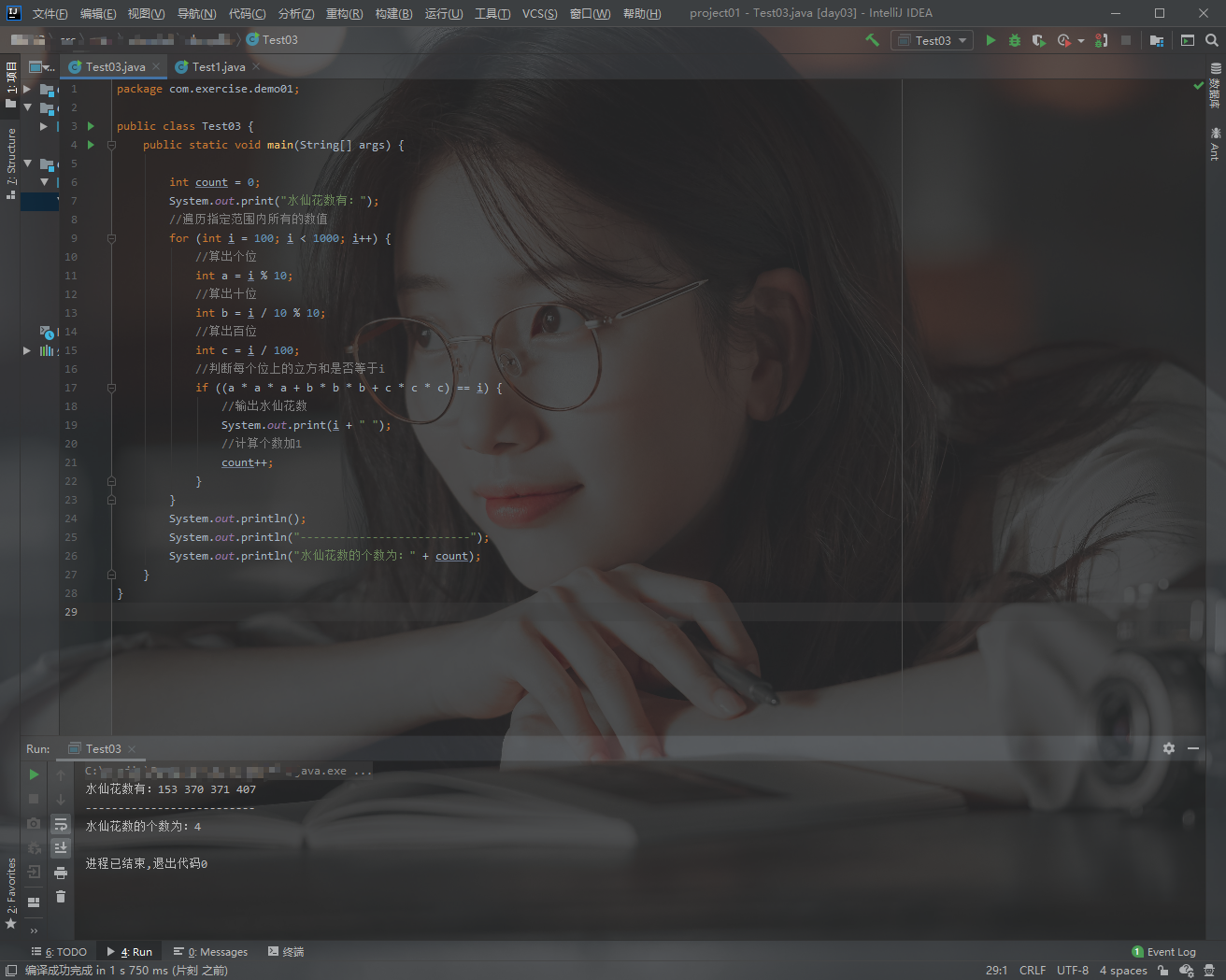
附：常见水仙花数

独身数共有9个: 1，2，3，4，5，6，7，8，9；

水仙花数共有4个：153，370，371，407；

四叶玫瑰数共有3个：1634，8208，9474；

五角星数共有3个：54748，92727，93084；

六合数只有1个：548834；

北斗七星数共有4个：1741725，4210818，9800817，9926315；

八仙数共有3个：24678050，24678051，88593477

……

​