luogu P1731 [NOI1999]生日蛋糕 |暴力枚举

题目背景

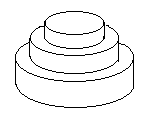
7月17日是Mr.W的生日，ACM-THU为此要制作一个体积为Nπ的M层

生日蛋糕，每层都是一个圆柱体。

设从下往上数第i(1<=i<=M)层蛋糕是半径为Ri, 高度为Hi的圆柱。当i<M时，要求Ri>Ri+1

由于要在蛋糕上抹奶油，为尽可能节约经费，我们希望蛋糕外表面（最下一层的下底面除外）的面积Q最小。

令Q= Sπ

请编程对给出的N和M，找出蛋糕的制作方案（适当的Ri和Hi的值），使S最小。

（除Q外，以上所有数据皆为正整数）

题目描述

输入格式

有两行，第一行为N（N<=20000），表示待制作的蛋糕的体积为Nπ；第二行为M(M<=15)，表示蛋糕的层数为M。

输出格式

仅一行，是一个正整数S（若无解则S=0）。

---

#include<iostream>
using namespace std;
int n,m;int maxn=(1<<31)-1;int f1[1001],f2[1001];
inline void dfs(int dep,int lastr,int lasth,int s,int v){
	if(dep==0){if(s<maxn&&n==v)maxn=s;return;}
	if(s+2*(n-v)/lastr>maxn)return;
	if(f1[dep]+v>n)return;
	if(f2[dep]+s>maxn)return;
	for(int r=min(n-v,lastr-1);r>=dep;r--)
	for(int h=min((n-v)/(r*r),lasth-1);h>=dep;h--)
	dfs(dep-1,r,h,2*r*h+s,v+r*r*h);

}
int main(){
    cin>>n>>m;
    for(int i=1;i<m;i++){f1[i]=i*i*i+f1[i-1];f2[i]=2*i*i+f2[i-1];}
    for(int r=n;r>=m;r--)
    for(int h=n/(r*r);h>=m;h--)
   	dfs(m-1,r,h,r*r+h*2*r,r*r*h);
	cout<<maxn;
}