DFS和BFS的比较

DFS（Depth First Search，深度优先搜索）和BFS（Breadth First Search，广度优先搜索）是两种典型的搜索算法。下面通过一个实例来比较一下深度优先搜索和广度优先搜索的搜索过程。

【例1】马的行走路径

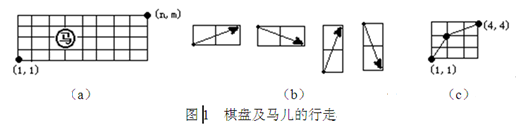
设有一个n*m的棋盘（2<=n<=50，2<=m<=50），在棋盘上任一点有一个中国象棋马，如图1（a）所示。马行走的规则为：（1）马走日字；（2）马只能向右走，即如图1（b）所示的4种走法。

编写一个程序，输入n和m，找出一条马从棋盘左下角（1，1）到右上角（n，m）的路径。例如：输入n=4、m=4时，输出路径 (1,1)->(2,3)->(4,4)。这一路经如图1（c）所示。若不存在路径，则输出"No！"

（1）编程思路。

将棋盘的横坐标规定为i，纵坐标规定为j，对于一个n×m的棋盘，i的值从1到n，j的值从1到m。棋盘上的任意点都可以用坐标（i，j）表示。

马有四种移动方向，每种移动方法用偏移值来表示，将这些偏移值分别保存在数组dx和dy中，可定义数组int dx[4]={1,1,2,2}和int dy[4]={-2,2,-1,1}。

定义数组int visit[51][51]标记某位置马儿是否已走过，初始时visit数组的所有元素值均为0，visit[i][j]=0表示坐标（i,j）处马儿未走过。同时为了后面输出路径方便，在标记visit[i][j]的值时，可以将其设置为其前一个位置的信息，例如visit[i][j] = x*100+y，它表示马儿由坐标（x,y）走到坐标（i,j）处。

（2）采用深度优先搜索编写的源程序。

#include <iostream>

using namespace std;

#define N 51

struct Node

{

int x;

int y;

};

int main()

{

int n,m;

int dx[4]={1,1,2,2};

int dy[4]={-2,2,-1,1};

int visit[N][N]={0};

Node s[N*N],cur,next; // s为栈

int top,i,x,y,t; // top为栈顶指针

cin>>n>>m;

top=-1; // 栈S初始化

cur.x=1; cur.y=1;

visit[1][1]=-1; // 点(1,1)为出发点，无前驱结点

s[++top]=cur; // 初始结点入栈；

bool flag= false; // 置搜索成功标志flag为假

while(top>=0 && !flag) // 栈不为空

{

cur=s[top--]; // 栈顶元素出栈

if (cur.x==n && cur.y==m)

{

flag=true;

x=n; y=m;

while (visit[x][y]!=-1)

{

cout<<"("<<x<<","<<y<<") <-- ";

t=visit[x][y];

x=t/100;

y=t%100;

}

cout<<"(1,1)"<<endl;

break;

}

for (i=0;i<4;i++)

{

x=cur.x+dx[i]; y=cur.y+dy[i];

if(x >=1 && x<=n && y>=0 && y<=m && visit[x][y]==0)

{

visit[x][y] = (cur.x)*100+cur.y; // 映射保存前驱结点信息

next.x=x; next.y=y; // 由cur扩展出新结点next

s[++top]=next; // next结点入栈

}

if (!flag)

cout<<"No path!"<<endl;

return 0;

}

为理解深度优先搜索的结点访问顺序，可以在上面源程序中的出栈语句后加上一条语句

cout<<"("<<cur.x<<","<<cur.y<<") -- "; 输出结点的出栈访问顺序。

（3）DFS的搜索过程。

以输入5,5为例，用树形结构表示马可能走的所有过程（如下图），求从起点到终点的路径，实际上就是从根结点开始搜索这棵树。

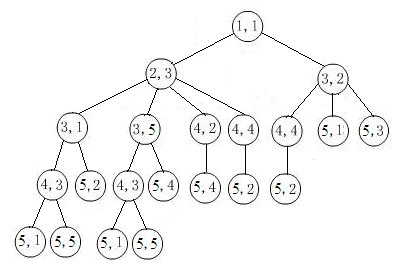
马从（1，1）开始，按深度优先搜索法，扩展出两个结点（2,3）和（3,2）依次入栈，之后（3,2）出栈，即走一步到达（3,2），判断是否到达终点，若没有，则继续往前走，扩展出结点（4,4）、（5,1）、（5,3）依次入栈，再走一步到达（5,3），没有到达终点，继续往前走，（5,3）的下一步所走的位置不在棋盘上，则另选一条路径再走；（5,1）出栈，即走到（5,1）；…，直到到达（5,5），搜索过程结束。

以输入5,5为例，输出的深度优先访问顺序为：

(1,1) -- (3,2) -- (5,3) -- (5,1) -- (4,4) -- (5,2) -- (2,3) -- (4,2) -- (5,4) -- (3,5) -- (4,3) -- (5,5)。

（4）采用广度优先搜索编写的源程序。

#include <iostream>

using namespace std;

#define N 51

struct Node

{

int x;

int y;

};

int main()

{

int n,m;

int dx[4]={1,1,2,2};

int dy[4]={-2,2,-1,1};

int visit[N][N]={0};

Node q[N*N],cur,next; // q为队列

int front,rear,i,x,y,t; // front为队头指针，rear队尾指针

cin>>n>>m;

front=rear=0; // 队列q初始化

cur.x=1; cur.y=1;

visit[1][1]=-1; // 点(1,1)为出发点，无前驱结点

q[rear++]=cur; // 初始结点入队

bool flag= false; // 置搜索成功标志flag为假

cout<<"结点访问顺序为：";

while(rear!=front && !flag) // 队列不为空

{

cur=q[front++]; // 队头元素出队

cout<<"("<<cur.x<<","<<cur.y<<") -- ";

if (cur.x==n && cur.y==m)

{

flag=true;

x=n; y=m;

cout<<endl;

cout<<"行走路径为：";