数据分析处理之PCA OLSR PCR PLSR(NIPALS)及其Matlab代码实现

传统的OLS(普通最小二乘)方法无法解决样本数据的共线性(multicollinearity)问题，如果你的数据样本中每个特征变量具有共线性，那么使用基于PCA的PCR和PLSR方法对数据样本进行回归建立模型将会是一个不错的选择。PCA是一种数据降维方式，但同时保持了原始数据降维后的特性；PCR是在降维后的数据空间(英文里常称为score)上进行OLSR(普通最小二乘回归)，然后将回归系数矩阵转化为原始空间；PLSR则可以看成改进版的PCR，该方法通过X和Y数据集的交叉投影方法使得回归模型兼顾到了X和Y数据集的本质关联，同时相比于PCR，在使用少数主成分的情况下具有更好的预测结果。

本文所有测试用数据集均来自Matlab，并使用Matlab封装的回归方法，对自己实现的代码做了验证，本文参考文献及资料如下：

Reference:

[1]   GELADI P, KOWALSKI B R. Partial least-squares regression: a tutorial [J]. Analytica chimica acta, 1986, 185(1-17).

[2]   WU F Y, ASADA H H. Implicit and intuitive grasp posture control for wearable robotic fingers: A data-driven method using partial least squares [J]. IEEE Transactions on Robotics, 2016, 32(1): 176-86.

[3]   https://en.wikipedia.org/wiki/Ordinary_least_squares

[4]   https://en.wikipedia.org/wiki/Principal_component_analysis

[5]   https://en.wikipedia.org/wiki/Principal_component_regression

[6]   https://en.wikipedia.org/wiki/Partial_least_squares_regression

[7]   https://github.com/scikit-learn/scikit-learn/blob/15a949460/sklearn/cross_decomposition/_pls.py#L502

完整Matlab代码实现: https://github.com/ShieldQiQi/PCA-PCR-PLSR-Matlab-code

---

一、OLSR

即为普通最小二乘回归，对此我们应该十分熟悉，各种大物材料力学实验都会用到这种方法，只不过我们当时使用的单变量的数据，当数据集涉及到矩阵，多维变量的形式时，就需要使用更加普遍适用的模型，我们设原始数据自变量(independent value)矩阵为$ X∈R_{n{\times}m} $，即X数据集含有n个样本，每个样本有m个特征变量；设原始数据因变量(dependent value)矩阵为$ Y∈R_{n{\times}p} $，即Y数据集含有n个样本，每个样本有p个特征变量。构建的最小二乘回归模型为：

$$ Y=X{\cdot}B+E \tag{1} $$

上式中$ B∈R_{m{\times}p} $为回归模型的系数矩阵，$ E∈R_{n{\times}p} $为模型预测的残差。B的通用解法参考维基百科，为：

$$ B=(X^{T}X)^{-1}X^{T}Y \tag{2} $$

二、PCA

PCA本质上是一种建立一种维度小于原始数据维度(特征变量数)正交基底空间，将原始数据投影到新的低维空间，以达到数据降维而保持原有特性的方法。PCA的步骤为：

1.对原始数据进行列居中处理: X(:,j) = X(:,j) - mean(X(:,j))

2.计算协方差矩阵$ X^{T}X $的前num大个特征值和对应的特征向量(此处num即为我们需要使用的主成分个数)

3.取前num个特征向量(作为列向量)组成系数矩阵P

4.通过公式 $  T=XP $ 即可求得在新空间下的降维后的(原来维度为m，降维后为num)数据矩阵T，英文里称为score，P称为loading

至于为什么这样做，PCA的原理可以参考维基百科，或者我的这篇博文:https://www.cnblogs.com/QiQi-Robotics/p/14303718.html

在实际应用中，计算协方差矩阵的特征向量常采用迭代计算的方式，常用的方法为NIPALS，Matlab精简代码(Matlab使用的为散布矩阵，而我的代码为协方差矩阵，所以特征值会相差(n-1)倍)实现如下：

 1 % 迭代得到num个成份
 2 for h = 1:num
 3     % step(1)
 4     % ---------------------------------------------------------------------
 5     % 取T(:,h)为任意一个X_centered中的列向量，此处直接取第一列
 6     T(:,h) = X_iteration(:,1);
 7
 8     % step(2) to step(5)
 9     % 迭代直到收敛到容忍度内的主成分
10     while(1)
11         P(:,h) = X_iteration'*T(:,h)/(T(:,h)'*T(:,h));
12         % 归一化P(:,h)
13         P(:,h) =  P(:,h)/sqrt(P(:,h)'*P(:,h));
14         t_temp = T(:,h);
15         T(:,h) = X_iteration*P(:,h)/(P(:,h)'*P(:,h));
16
17         % 检查当前T(:,h)与上一步T(:,h)是否相等以决定是否继续迭代
18         if max(abs(T(:,h)-t_temp)) <= tolerance
19             % 存储按顺序排列的特征值
20             % 注意此处的特征值为协方差矩阵的特征值，而matlab PCA方法使用的为散布矩阵(离散度矩阵)，故后者的特征值为前者的(n-1)倍
21             eigenValues(h) = P(:,h)'*(X_centered'*X_centered)*P(:,h);
22             break;
23         else
24         end
25     end
26
27     % 计算残差，更新数据矩阵
28     % ---------------------------------------------------------------------
29     X_iteration = X_iteration - T(:,h)*P(:,h)';
30 end

三、PCR

PCR使用的回归方法是OLSR，只不过回归的模型是建立在主成分空间，以防止原始数据的共线性问题导致模型建立不准确，步骤如下：

1.执行PCA对原始数据进行降维处理

2.对新数据矩阵T(score)(选多少列，就是利用多少个主成分)和居中(mean-centered)后的Y建立OLSR回归模型，得到主成分空间中的回归系数矩阵$ B^{'} $

3.最终原始空间的系数矩阵$ B=P{\cdot}B^{'} $，该步可以将 $ T=XP $ 代入到式(1)中推导而得(利用$ PP^{T}=E $)

4.当我们需要回归新的到的数据X*时，将该数据对减去原始模型数据X的均值，代入到回归模型，得到预测的$Y^{'}$，然后该矩阵加上原始模型数据Y的均值即为最终的结果

Matlab精简代码如下：

 1 % 定义测试集样本的数量
 2 r = n;
 3 % 将原始数据降维到主成分空间(T)后，使用OLS最小二乘回归获取系数矩阵
 4 B_inPca = inv(T'*T)*T'*Y_centered;
 5 %B_inPca = regress(Y-mean(Y), T(:,1:num));
 6 % 将系数矩阵从主成分空间转化到原始空间
 7 B_estimated = P*B_inPca;
 8
 9 % 定义测试集，此处直接使用原始数据的前r行
10 X_validate = zeros(r,m);
11 % 对原始数据集居中列平均化
12 for j = 1:m
13     % 注意，此处减去的平均值应该为模型数据集的平均值，而非新数据的平均值
14     X_validate(:,j) =   X(1:r,j) - mean(X(:,j));
15 end
16
17 Y_estimated = X_validate*B_estimated;
18 for i = 1:p
19    % 注意此处最终的输出需要加上数据集Y的均值
20    Y_estimated(:,i) = Y_estimated(:,i) + mean(Y(:,i));
21 end

四、PLSR

PLSR相对于PCR的一个优点在于在使用更少的主成分可以获得更具有鲁棒性的预测结果(具体可以查看Matlab中关于PLSR的帮助文档)，具体步骤查阅论文 [1]。精简版Matlab代码如下：

1.建立模型部分

 1 % 迭代得到num个成份
 2 for h = 1:num
 3     % step(1)
 4     % ---------------------------------------------------------------------
 5     % 取u_h为任意一个Y_centered中的列向量，此处直接取第一列
 6     U(:,h) = Y_centered(:,1);
 7
 8     % step(2) to step(8)
 9     % ---------------------------------------------------------------------
10     while 1
11         % 在数据矩阵X_centered中
12         W(:,h) = X_centered'*U(:,h)/(U(:,h)'*U(:,h));
13         % 对数据进行归一化
14         W(:,h) = W(:,h)/sqrt(W(:,h)'*W(:,h));
15         t_temp = T(:,h);
16         T(:,h) = X_centered*W(:,h)/(W(:,h)'*W(:,h));
17
18         % 在数据矩阵Y_centered中
19         Q(:,h) = Y_centered'*T(:,h)/(T(:,h)'*T(:,h));
20         % 对数据进行归一化
21         Q(:,h) = Q(:,h)/sqrt(Q(:,h)'*Q(:,h));
22         U(:,h) = Y_centered*Q(:,h)/(Q(:,h)'*Q(:,h));
23
24         % 检查T(:,h)与T(:,h)的前一步是否相等，若小于某个数值则该PLS成份迭代完成，否则返回继续迭代
25         if max(abs(T(:,h)-t_temp)) <= tolerance
26             break;
27         else
28         end
29     end
30
31     % step(9) to step(13)
32     % ---------------------------------------------------------------------
33     P(:,h) = X_centered'*T(:,h)/(T(:,h)'*T(:,h));
34     % 对数据进行归一化
35     p_norm = sqrt(P(:,h)'*P(:,h));
36     P(:,h) = P(:,h)/p_norm;
37     T(:,h) = T(:,h)*p_norm;
38     W(:,h) = W(:,h)*p_norm;
39     B(h) = U(:,h)'*T(:,h)/(T(:,h)'*T(:,h));
40
41     % 计算残差，更新数据矩阵
42     % ---------------------------------------------------------------------
43     X_centered = X_centered - T(:,h)*P(:,h)';
44     Y_centered = Y_centered - B(h)*T(:,h)*Q(:,h)';
45 end

2.预测部分

 1 % 对原始数据集居中列平均化
 2 for j = 1:m
 3     % 注意，此处减去的平均值应该为模型数据集的平均值，而非新数据的平均值
 4     X_validate(1:r,j) =   X(1:r,j) - mean(X(:,j));
 5 end
 6
 7 % 计算预测的T
 8 for h = 1:num
 9     T_est(:,h) = X_validate*W(:,h);
10     X_validate = X_validate - T_est(:,h)*P(:,h)';
11 end
12
13 % 计算预测的Y
14 for h = 1:num
15     Y_estimated = Y_estimated + B(h)*T_est(:,h)*Q(:,h)';
16 end
17 for i = 1:p
18    % 注意此处最终的输出需要加上数据集Y的均值
19    Y_estimated(:,i) = Y_estimated(:,i) + mean(Y(:,i));
20 end

五、实验结果

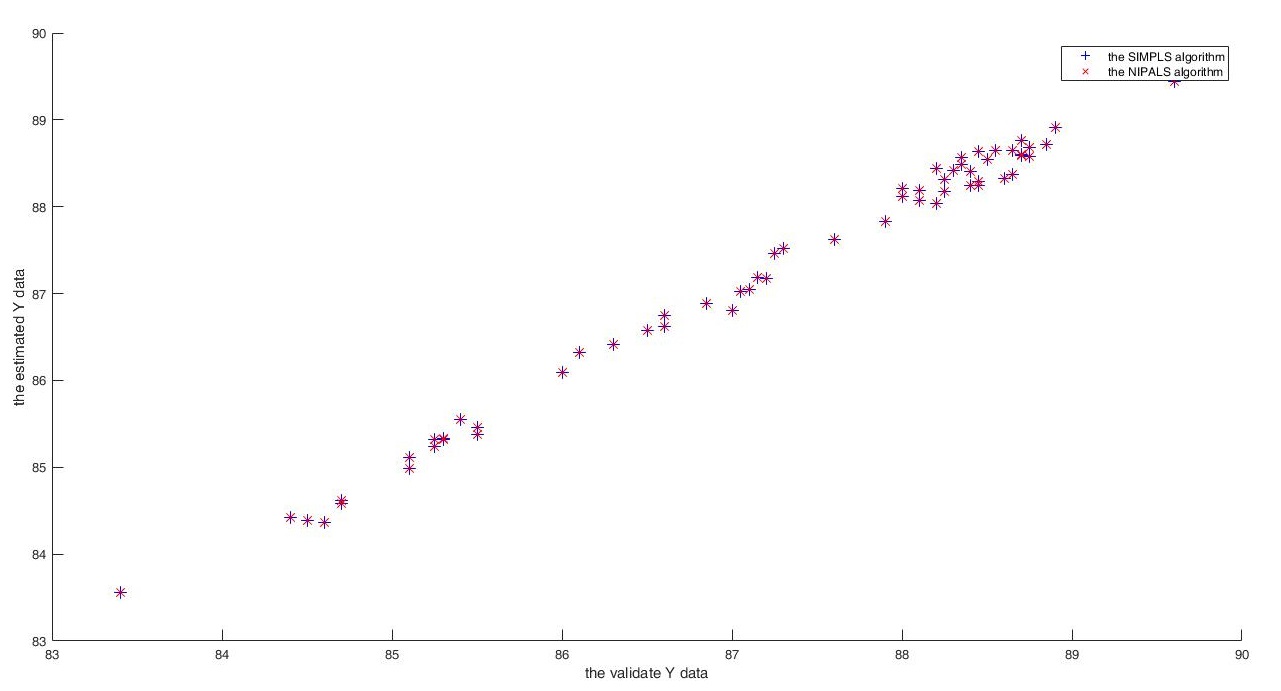
图1 Matlab PLSR算法(SIMPLS)和自定义PLSR(NIPALS)方法效果对比