BUAA_2019_OO_第一单元总结

一、基于度量来分析自己的程序结构

1、第一次作业

1.1类图：

　　

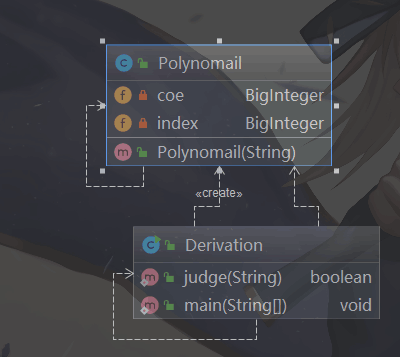
　　第一次作业由于比较简单，我采用了面向过程的编程方式。在Polynomail类的构造函数中将项直接求导输出。这样的弊端显而易见，不能进行优化。

1.2复杂度分析

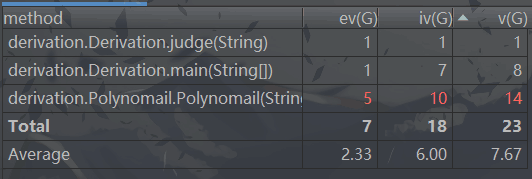
　　由于在Polynomail类的构造函数中直接求导，构造函数复杂度最高。

1.3总结反思

　　第一次作业属于投机取巧的反面教材，面向过程编程的错误显而易见。应该用Arraylist将建造的类存起来，再在Polynomial类中写求导方法，这样既符合面向对象的编程思想，又便于优化

2、第二次作业

2.1类图

　　第二次作业在第一次作业的基础上做了改进，采用如下思路：

　　

2.2复杂度分析

　　这次将求导单独成类，正则表达式匹配format先去空格。复杂度最高的仍然是这两个方法。

2.3总结反思

　　第二次作业仍然属于偷懒，在讨论区学习到了这种方法后做了一定的改进。由于没有建立幂函数类和三角函数类，无形中给第三次作业增加了许多难度。

3、第三次作业

　　第三次作业没有通过中测，由于前两次没有建立起面向对象的编程思想，在第三次作业中我尝试使用面向过程进行求导，但过于复杂没有实现。

二、自己程序的bug

1、第一次作业

　　第一次作业的bug主要来源于format。由于采用暴力正则表达式匹配，导致正则表达式十分复杂。在检查时发现在符号 x 和 ^ 之间没有添加空格，是粗心导致的bug。其次关于正则匹配爆栈的问题，经讨论区大佬推荐，参考了该文：https://blog.csdn.net/weixin_42516949/article/details/80858913。

2、第二次作业

　　第二次作业在建立Term类的时候对于字符串的处理出现了失误。在 为-x 和 +x 建立类的时候没有将常数 +1 和 -1分离出来，而后在将字符串转化为BigInteger类型的数字时程序抛出异常。这个异常在Term类的x1Add方法中抛出，但实际需要修改的时Dervation类的change函数中。

三、发现别人程序bug所采用的策略

　　一开始我选择阅读每一个人的代码来找出别人的bug，但这样的工作量实在太大。后来我转变思路，先从自己写代码时遇到的困难和出现的bug入手，优先测试别人程序中有没有解决这些问题或者是否还存在着我遇到过的bug。在讨论课上有大佬分享了自己使用对拍器进行互测的过程，受益颇多，以后可以尝试这种方法。

四、总结

　　本单元作业难度递增，前面两次作业在为第三次作业铺路，然而偷懒的小学生并没有意识到课程组用心良苦的安排，在前两次作业中摸水，直接导致第三次作业爆炸。错过了第三次作业面向对象的洗礼，后面只能面对更大的挑战。