【数据结构与算法Python版学习笔记】算法分析

什么是算法分析

• 算法是问题解决的通用的分步的指令的聚合
• 算法分析主要就是从计算资源的消耗的角度来评判和比较算法。

计算资源指标

• 存储空间或内存
• 执行时间

影响算法运行时间的其他因素

• 分为最好、最差和平均情况，平均状况体现主流性能

累计求和案例

import time
def sumOFN2(n):
    start=time.time()
    theSum=0
    for i in range(1,n+1):
        theSum+=i
    end=time.time()
    return theSum,end-start
def sumOFN3(n):
    start=time.time()
    theSum=(n*(n+1))/2
    end=time.time()
    return theSum,end-start
if __name__ == "__main__":
    for i in range(5):
        print("sum is %d required %10.7f seconds" % sumOFN2(100000))
    print("--------")
    for i in range(5):
        print("sum is %d required %10.7f seconds" % sumOFN3(100000))
-----------
sum is 5000050000 required  0.1255534 seconds
sum is 5000050000 required  0.1245010 seconds
sum is 5000050000 required  0.1389964 seconds
sum is 5000050000 required  0.1279476 seconds
sum is 5000050000 required  0.1276410 seconds
--------
sum is 5000050000 required  0.0000000 seconds
sum is 5000050000 required  0.0000000 seconds
sum is 5000050000 required  0.0000000 seconds
sum is 5000050000 required  0.0000000 seconds
sum is 5000050000 required  0.0000000 seconds

“大O” 表示法

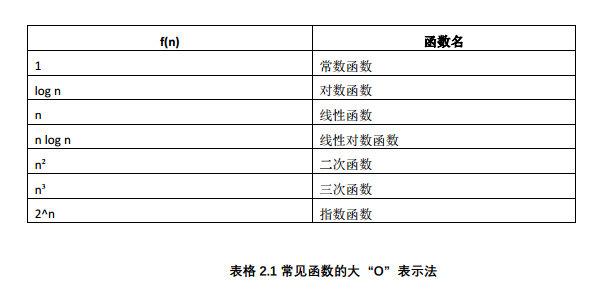
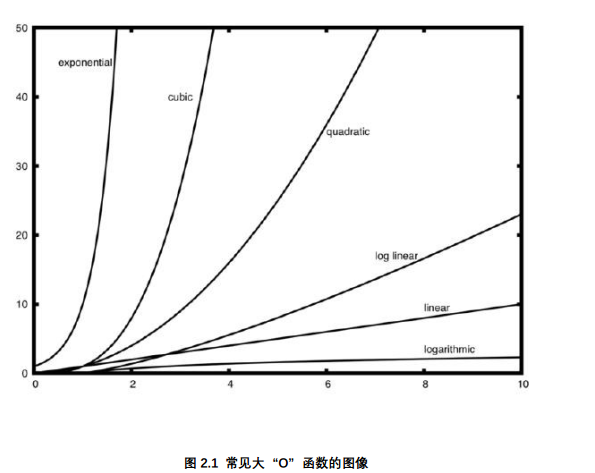
• 数量级函数用来描述当规模 n 增加时， T(n)函数中增长最快的部分。

• 常见大O表示法

  

  

变 位 词 检 测

如果一个字符串是另一个字符串的重新排列组合，那么这两个字符串互为变位词。比如， ”heart”与”earth”互为变位词， ”python”与”typhon”也互为变位词。

• 逐字检查法 O(n²)
• 排序比较法 O(nlogn)
• 暴力匹配算法 O(n!)
• 字母计数比较法 O(n)

#变位词判断问题
#逐字检查
def anagramSolution(s1,s2):
    alist=list(s2)
    pos1=0
    stillOK=True
    while pos1<len(s1) and stillOK:#循环s1中的每一个字符
        pos2=0
        found=False
        while pos2<len(alist) and not found:
            if s1[pos1]==alist[pos2]:
                found=True
            else:
                pos2=pos2+1
        if found:
            alist[pos2]=None
        else:
            stillOK=False
        pos1=pos1+1
    return stillOK
#print(anagramSolution('abcd','dcba'))
#排序解法
def anagramSolution2(s1,s2):
    alist1=list(s1)
    alist2=list(s2)
    alist1.sort()
    alist2.sort()
    pos=0
    matches=True
    while pos<len(s1) and matches:
        if alist1[pos]==alist2[pos]:
            pos=pos+1
        else:
            matches=False
    return matches
print(anagramSolution2('abcd','dcba'))
#计数器解法
def anagramSolution3(s1,s2):
    c1=[0]*26
    c2=[0]*26
    for i in range(len(s1)):
        pos=ord(s1[i])-ord('a')#把a-z转化为0-25   ps:感谢m0_47550366的提醒，此处错误已改正
        c1[pos]=c1[pos]+1#计数
    for i in range(len(s2)):
        pos = ord(s2[i]) - ord('a')  # 把a-z转化为0-25
        c2[pos] = c2[pos] + 1  # 计数
    j=0
    stillOK=True
    while j<26 and stillOK:
        if c1[j]==c2[j]:
            j=j+1
        else:
            stillOK=False
    return stillOK
print(anagramSolution3('abcd','dcba'))

python数据类型

List 列表

```python
import timeit # 运行时间测量模块
from timeit import Timer
# 循环连接
def test1():
    l=[]
    for i in range(1000):
        l=l+[i]
# append添加
def test2():
    l=[]
    for i in range(1000):
        l.append(i)
# 列表推导式
def test3():
    l=[i for i in range(1000)]
# range转列表
def test4():
    l=list(range(1000))
if __name__ == "__main__":
    t1=Timer("test1()","from __main__ import test1")
    print("concat %f second" % t1.timeit(number=1000)) # number指定程序被执行的次数
    t2=Timer("test2()","from __main__ import test2")
    print("append %f second" % t2.timeit(number=1000)) 
    t3=Timer("test3()","from __main__ import test3")
    print("comprehension %f second" % t3.timeit(number=1000)) 
    t4=Timer("test4()","from __main__ import test4")
    print("list range %f second" % t4.timeit(number=1000))
-------
concat 1.979591 second
append 0.811599 second
comprehension 0.375291 second
list range 0.024658 second
```

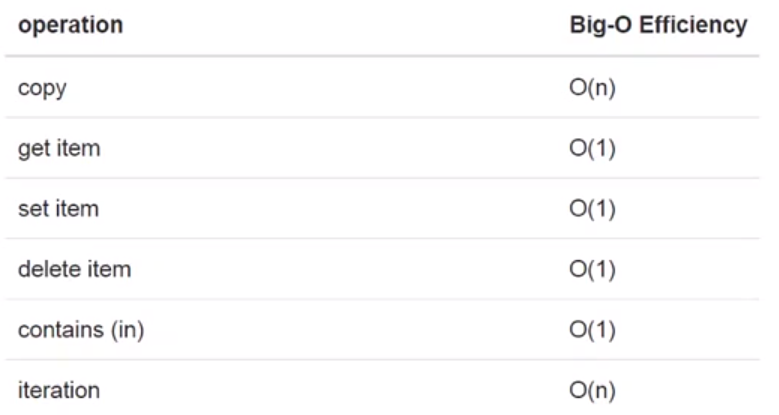
dict 字典