bzoj千题计划270：bzoj4559: [JLoi2016]成绩比较（拉格朗日插值）

http://www.lydsy.com/JudgeOnline/problem.php?id=4559

f[i][j] 表示前i门课，有j个人没有被碾压的方案数

g[i] 表示第i门课，满足B神排名的分数安排方案数

g[i]的求法：

枚举B神这门课x分，则有n-Ri个人的分数<=x ，Ri-1个人的分数>x

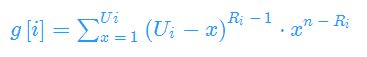
Ui 上限是1e9，但是g[i] 是一个关于Ui 的n次多项式，所以可以用拉格朗日插值法来求

递推 f[i][j]：

假设f[i-1][w] 转移到了f[i][j]，j>=w

前i-1门课没有被碾压，前i门课也一定没有被碾压

前i-1门课被碾压，前i门课可能继续被碾压，也可能不再被碾压

单看这一门课有Ri-1个人的成绩比B神高

但这Ri-1个人之前可能就有科目比B神高，已经不被碾压，这次成绩比B神高还是低都行

所以实际新增加了j-w个没有被碾压的，即这j-w个人这一门的成绩比B神高，之前的科目都比B神低

在已经没有被碾压的w个人中，还存在 Ri-1-（j-w）个人的成绩比B神高

之前有n-w-1个人被碾压，所以新增情况的方案数为C（n-w-1，j-w）

后一种情况的方案数为C（w，Ri-1-j+w）

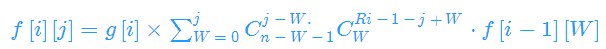
#include<cstdio>

#include <iostream>

using namespace std;

const int mod=1e9+;

#define N 101

int C[N][N];

int U[N],rk[N];

int f[N][N];

int g[N];

void read(int &x)

{

    x=; char c=getchar();

    while(!isdigit(c)) c=getchar();

    while(isdigit(c)) { x=x*+c-''; c=getchar(); }

}

int get_C(int n,int m)

{

    if(n< || m< || n<m) return ;

    return C[n][m];

}

void pre_C()

{

    C[][]=;

    for(int i=;i<=;++i)

    {

        C[i][]=;

        for(int j=;j<=i;++j)

            C[i][j]=(C[i-][j-]+C[i-][j])%mod;

    }

}

int Pow(int a,int b)

{

    int res=;

    for(;b;a=1LL*a*a%mod,b>>=)

        if(b&) res=1LL*res*a%mod;

    return res;

}

int Langrange(int n,int r,int k)

{

    for(int u=;u<=k;++u)

    {

        g[u]=;

        for(int x=;x<=u;++x)

            g[u]=(g[u]+1LL*Pow(u-x,r-)*Pow(x,k--r)%mod)%mod;

        if(n==u) return g[u];

    }

    int fz=;

    for(int i=;i<=k;++i) fz=1LL*fz*(n-i)%mod;

    int fm,ans=;

    for(int i=;i<=k;++i)

    {

        fm=n-i;

        for(int j=;j<=k;++j)

            if(i!=j) fm=1LL*fm*(i-j)%mod;

        ans=(ans+1LL*fz*g[i]%mod*Pow(fm,mod-)%mod)%mod;

    }

    if(ans<) ans+=mod;

    return ans;

}

int main()

{

    int n,m,k;

    read(n); read(m); read(k);

    for(int i=;i<=m;++i) read(U[i]);

    for(int i=;i<=m;++i) read(rk[i]);

    pre_C();

    int G;

    f[][]=;

    for(int i=;i<=m;++i)

    {

        G=Langrange(U[i],rk[i],n+);

        for(int j=;j<=n;++j)

        {

            for(int w=;w<=j;++w)

                f[i][j]=(f[i][j]+1LL*f[i-][w]*get_C(w,rk[i]--j+w)%mod*get_C(n-w-,j-w)%mod)%mod;

            f[i][j]=1LL*f[i][j]*G%mod;

        }

    }

    printf("%d",f[m][n-k-]);

    return ;

}

4559: [JLoi2016]成绩比较

Time Limit: 20 Sec Memory Limit: 256 MB
Submit: 366 Solved: 211
[Submit][Status][Discuss]

Description

G系共有n位同学，M门必修课。这N位同学的编号为0到N-1的整数，其中B神的编号为0号。这M门必修课编号为0到M-

1的整数。一位同学在必修课上可以获得的分数是1到Ui中的一个整数。如果在每门课上A获得的成绩均小于等于B获

得的成绩，则称A被B碾压。在B神的说法中，G系共有K位同学被他碾压（不包括他自己），而其他N-K-1位同学则没

有被他碾压。D神查到了B神每门必修课的排名。这里的排名是指：如果B神某门课的排名为R，则表示有且仅有R-1

位同学这门课的分数大于B神的分数，有且仅有N-R位同学这门课的分数小于等于B神（不包括他自己）。我们需要

求出全系所有同学每门必修课得分的情况数，使其既能满足B神的说法，也能符合D神查到的排名。这里两种情况不

同当且仅当有任意一位同学在任意一门课上获得的分数不同。你不需要像D神那么厉害，你只需要计算出情况数模1

0^9+7的余数就可以了。

Input

第一行包含三个正整数N,M,K，分别表示G系的同学数量（包括B神），必修课的数量和被B神碾压的同学数量。第二

行包含M个正整数，依次表示每门课的最高分Ui。第三行包含M个正整数，依次表示B神在每门课上的排名Ri。保证1

≤Ri≤N。数据保证至少有1种情况使得B神说的话成立。N<=100,M<=100,Ui<=10^9

Output

仅一行一个正整数，表示满足条件的情况数模10^9+7的余数。

Sample Input

3 2 1
2 2
1 2

Sample Output