bzoj4289 Tax
Description
Sample Input
1 2 5
1 3 2
2 3 1
2 4 4
3 4 8
Sample Output
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <queue>
#include <cstdlib>
#define REP(i,k,n) for(int i=k;i<=n;i++)
#define in(a) a=read()
#define MAXN 400040
using namespace std;
inline int read(){
int x=,f=;
char ch=getchar();
for(;!isdigit(ch);ch=getchar())
if(ch=='-')
f=-;
for(;isdigit(ch);ch=getchar())
x=x*+ch-'';
return x*f;
}
int n,m;
int S,T;
int total,head[MAXN],to[MAXN*],nxt[MAXN*],val[MAXN*];
int Total,Head[],To[],Nxt[],Val[];
int vis[];
long long dis[];
struct edge{
int id,va;
}st[MAXN*];
struct node{
int a;
long long b;
bool operator <(const node &x)const{
return b>x.b;
}
};
priority_queue<node> Q;
inline int change(int x){
if(x%==) return x+;
return x-;
}
inline void adl(int a,int b,int c){
total++;
to[total]=b;
val[total]=c;
nxt[total]=head[a];
head[a]=total;
return ;
}
inline void Adl(int a,int b,int c){
Total++;
To[Total]=b;
Val[Total]=c;
Nxt[Total]=Head[a];
Head[a]=Total;
return ;
}
inline bool cmp(edge a,edge b){
return a.va<b.va;
}
inline void solve(int u){
int cnt=;
for(int e=head[u];e;e=nxt[e]) st[++cnt].id=e,st[cnt].va=val[e];
sort(st+,st+cnt+,cmp);//对于u的所有出边排序
REP(i,,cnt-) Adl(st[i].id,st[i+].id,st[i+].va-st[i].va),Adl(st[i+].id,st[i].id,);//连查分边
for(int e=head[u];e;e=nxt[e]) Adl(change(e),e,val[e]);//每一条出边连向所对入边
return ;
}
inline long long Dijkstra(){
memset(dis,0x7f,sizeof(dis));
dis[S]=;
node p;
p.a=S,p.b=;
Q.push(p);
while(!Q.empty()){
int u=Q.top().a;Q.pop();
if(vis[u]) continue;
vis[u]=;
for(int e=Head[u];e;e=Nxt[e])
if(dis[To[e]]>dis[u]+Val[e]){
dis[To[e]]=dis[u]+Val[e];
node q;
q.a=To[e],q.b=dis[To[e]];
Q.push(q);
}
}
return dis[T];
}
int main(){
in(n),in(m);
int a,b,c;
REP(i,,m) in(a),in(b),in(c),adl(a,b,c),adl(b,a,c);
S=,T=total+;
for(int e=head[];e;e=nxt[e]) Adl(S,e,val[e]);//处理源点
for(int e=head[n];e;e=nxt[e]) Adl(change(e),T,val[e]);//处理汇点
for(int i=;i<=n;i++) solve(i);
printf("%d",Dijkstra());
return ;
}
/*
4 5
1 2 5
1 3 2
2 3 1
2 4 4
3 4 8
*/
bzoj4289 Tax的更多相关文章
- BZOJ4289 Tax 最短路建模
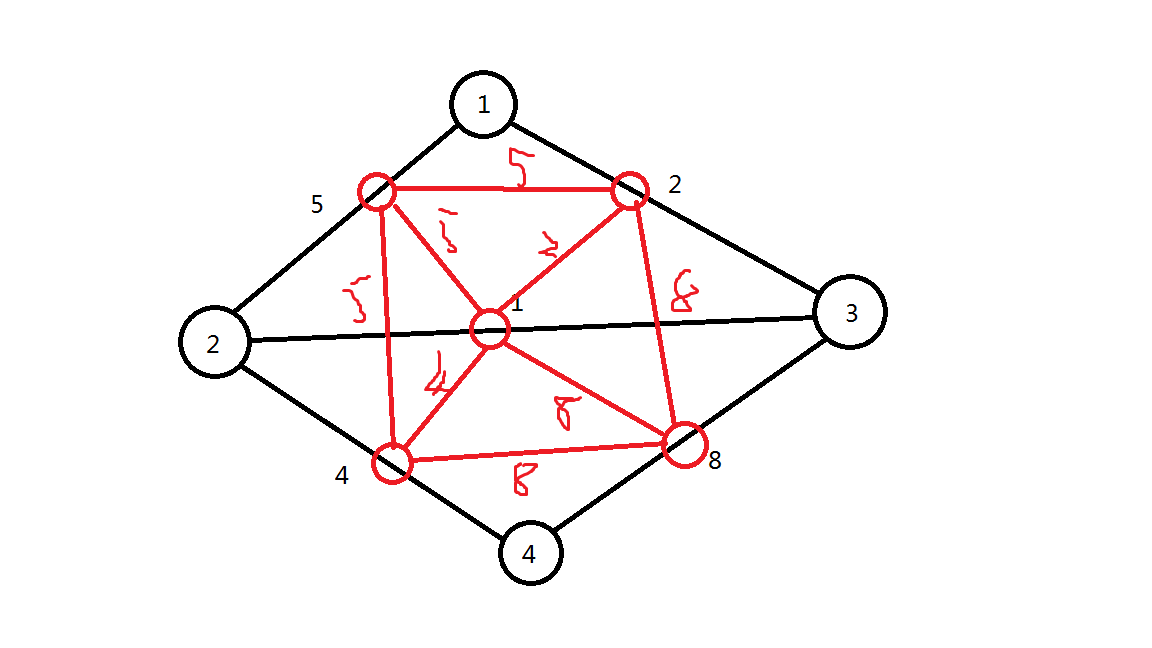
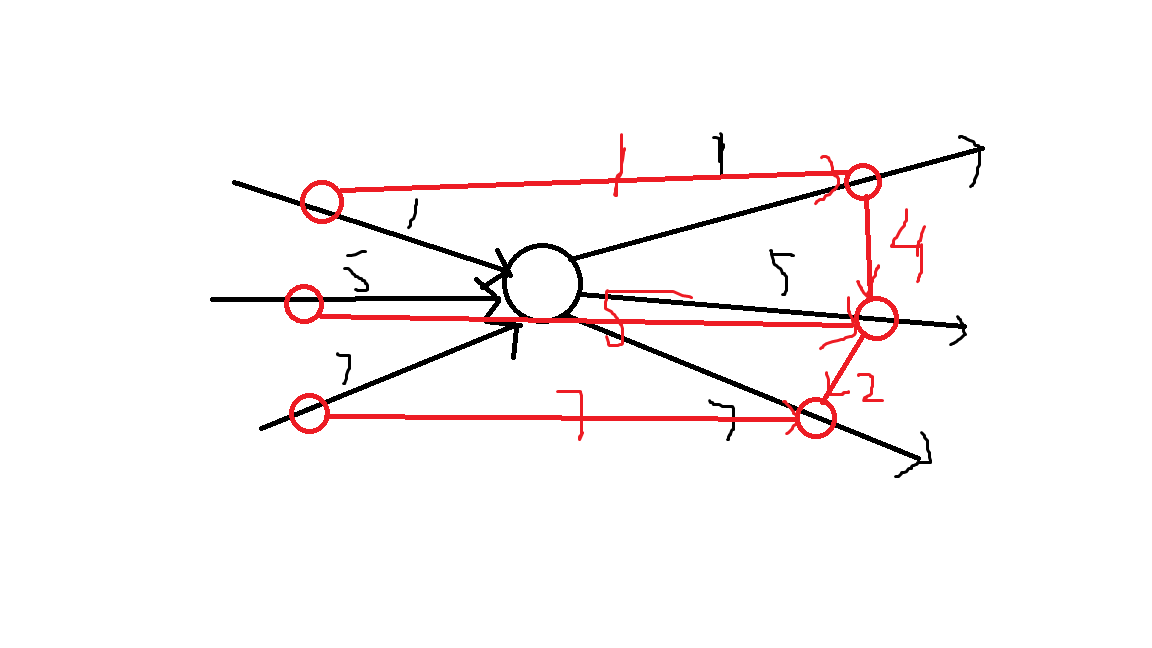
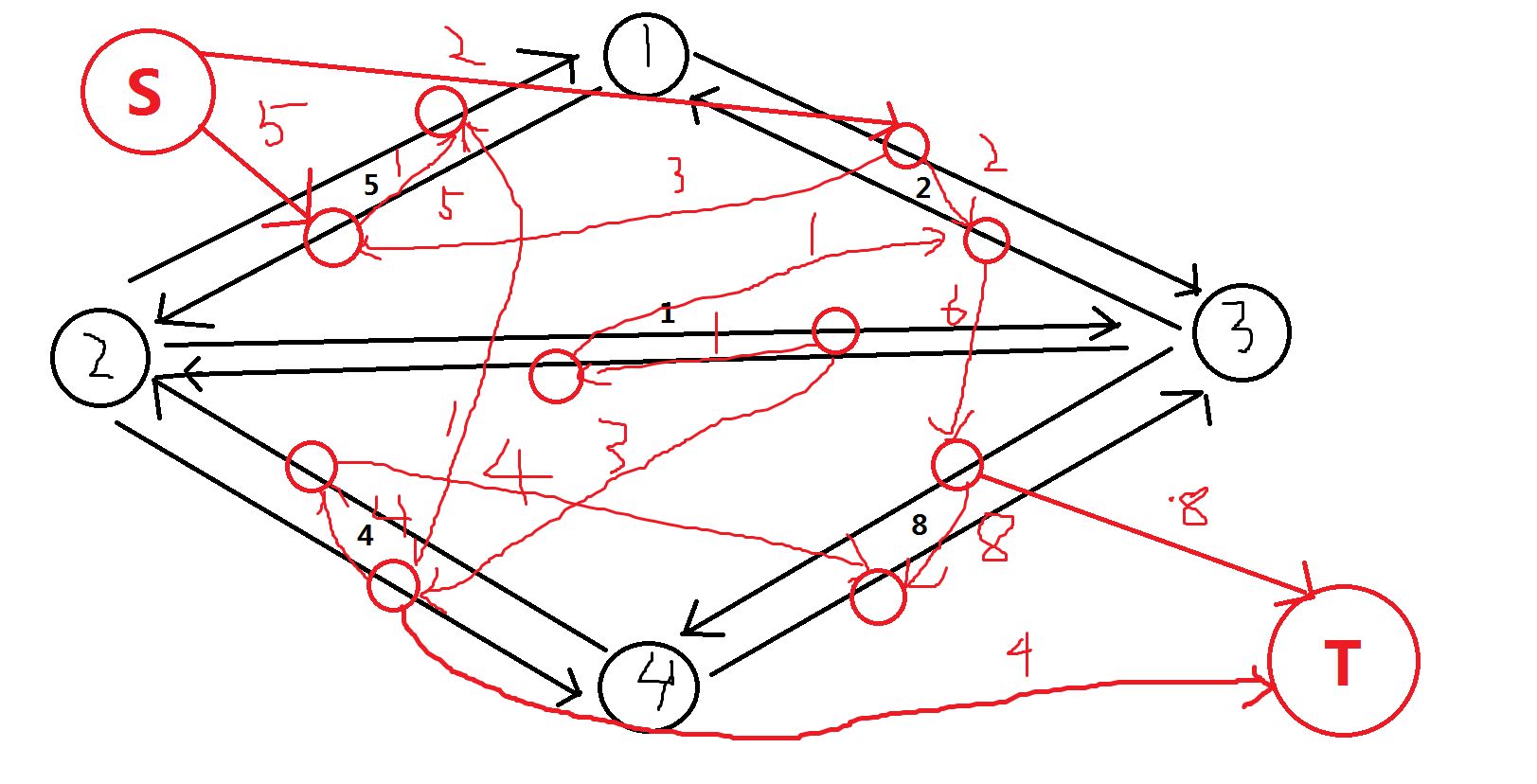
给定一个带边权的无向图,求1到n的最小代价路径.经过一个点的代价是路径上这个点的入边和出边的较大权值. \(n \le 100000, m \le 200000\). 一般的建图是考虑每个点,其入边和 ...
- 【BZOJ-4289】Tax 最短路 + 技巧建图
4289: PA2012 Tax Time Limit: 10 Sec Memory Limit: 128 MBSubmit: 168 Solved: 69[Submit][Status][Dis ...
- [BZOJ4289] [PA2012] Tax 解题报告 (最短路+差分建图)
题目链接:https://www.lydsy.com/JudgeOnline/problem.php?id=4289 4289: PA2012 Tax Time Limit: 10 Sec Memo ...
- BZOJ4289 : PA2012 Tax
一个直观的想法是把每条边拆成两条有向边,同时每条有向边是新图中的一个点.对于两条边a->b与b->c,两点之间连有向边,费用为两条边费用的最大值.然后新建源点S与汇点T,由S向所有起点为1 ...
- [BZOJ4289][PA2012]TAX(最短路)
首先考虑一种暴力做法,为每条边拆成两条有向边,各建一个点.若某两条边有公共点,则在边所对应的点之间连一条边,权值为两条边中的较大值.这样跑最短路是$O(m^2\log m)$的. 用类似网络流中补流的 ...
- [Bzoj4289]PA2012 Tax(Dijkstra+技巧建图)
Description 给出一个N个点M条边的无向图,经过一个点的代价是进入和离开这个点的两条边的边权的较大值,求从起点1到点N的最小代价.起点的代价是离开起点的边的边权,终点的代价是进入终点的边的边 ...
- 【PA2012】【BZOJ4289】Tax
Description 给出一个N个点M条边的无向图,经过一个点的代价是进入和离开这个点的两条边的边权的较大值.求从起点1到点N的最小代价. 起点的代价是离开起点的边的边权.终点的代价是进入终点的边的 ...
- bzoj4289 PA2012 Tax——点边转化
题目:https://www.lydsy.com/JudgeOnline/problem.php?id=4289 好巧妙的转化!感觉自己难以想出来... 参考了博客:https://blog.csdn ...
- 【BZOJ-4289】Tax 最短路 + 技巧建图(化边为点)
题意 给出一个N个点M条边的无向图,经过一个点的代价是进入和离开这个点的两条边的边权的较大值,求从起点1到点N的最小代价.起点的代价是离开起点的边的边权,终点的代价是进入终点的边的边权N<=10 ...
随机推荐
- Linux - seq 预设外部命令
seq 是Linux 中一个预设的外部命令,一般用作一堆数字的简化写法. 常用参数: # 不指定起始数值,则默认为 1 -s # 选项主要改变输出的分格符, 预设是 \n -w # 等位补全,就是宽度 ...
- 第6月第10天 svn checkout sqlite3
1. http://www.cnblogs.com/xuling/p/5602036.html 2. http://blog.csdn.net/qq_26819733/article/details/ ...
- 关于cookie和session
在设置cookie的时候,它会保留在本地,无论你有没有退出浏览器都是.但是session只能在登录状态有效.退出浏览器过后就会消除掉.同时设置也是有问题的. @app.route('/login',m ...
- vue实践中的狗血事件之:mock数据引发的血坑
在项目实践中,遇到了这么一档子事 开发环境下,很快乐,什么事儿都没有,于是想打包一下测一下自动登录的效果 好家伙,一开始登录没有效,改来改去,最后连路由都切换不了, 明明开发环境下好好的,为毛打包后就 ...
- mongoexport导出csv中文乱码
在用mongoexport导出csv文件时,发现数据库中的中文在excel中都显示为乱码,用notepad打开则正常. 解决办法: 在notepad中,将编码格式改为UTF-8,保存,再用excel打 ...
- 008_MAC 终端使用技巧
一.常用终端命令. <1>reset 的作用很简单——将目前「终端」屏幕上的内容清空,就好像刚刚打开终端一样. <2>如果你在一条终端命令中发现有输入错误的话,那么用 cont ...
- JMeter出现“the target server failed to respond“的解决办法
今天用jmeter压测执行过程中遇到一个报错如下: 解决方案如下: 1. 修改执行计划中,HTTP请求的Implementation为HttpClient4. 2. 保存执行计划 3. 修改JMete ...
- 09 Go 1.9 Release Notes
Go 1.9 Release Notes Introduction to Go 1.9 Changes to the language Ports ppc64x requires POWER8 Fre ...
- 再谈CentOS 7程序自启动
上次发现了/etc/init.d下已经没有启动脚本了,然后对于启动乱序自己在rc.local中重排. 其实想一想这些应用的自启动终归还是需要通过脚本来执行的. 一.脚本在哪里? /usr/lib/sy ...
- JDK7的新玩具java.util.Objects
空指针异常这个坑爹的异常是初学开发者最常见的坑,那么今天为大家分享一个jdk的新工具java.util.Objects包.里面有很多工具可以帮我们避免空指针异常让我我们的代码写起来更加优雅.下面我们来 ...
