HDU 5212 Code (莫比乌斯反演)

题意：给定上一个数组，求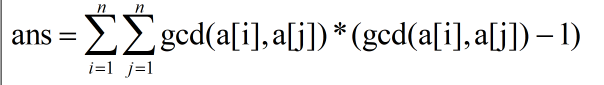

析：

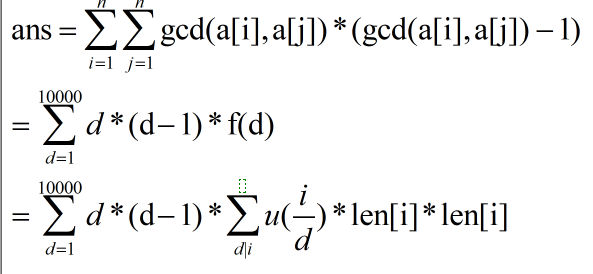
其中，f(d)表示的是gcd==d的个数，然后用莫比乌斯反演即可求得，len[i]表示能整队 i 的个数，可以线性筛选得到，

代码如下：

#pragma comment(linker, "/STACK:1024000000,1024000000")
#include <cstdio>
#include <string>
#include <cstdlib>
#include <cmath>
#include <iostream>
#include <cstring>
#include <set>
#include <queue>
#include <algorithm>
#include <vector>
#include <map>
#include <cctype>
#include <cmath>
#include <stack>
#include <sstream>
#include <list>
#include <assert.h>
#include <bitset>
#include <numeric>
#define debug() puts("++++")
#define gcd(a, b) __gcd(a, b)
#define lson l,m,rt<<1
#define rson m+1,r,rt<<1|1
#define fi first
#define se second
#define pb push_back
#define sqr(x) ((x)*(x))
#define ms(a,b) memset(a, b, sizeof a)
#define sz size()
#define pu push_up
#define pd push_down
#define cl clear()
#define lowbit(x) -x&x
//#define all 1,n,1
#define FOR(i,x,n)  for(int i = (x); i < (n); ++i)
#define freopenr freopen("in.txt", "r", stdin)
#define freopenw freopen("out.txt", "w", stdout)
using namespace std;

typedef long long LL;
typedef unsigned long long ULL;
typedef pair<int, int> P;
const int INF = 0x3f3f3f3f;
const LL LNF = 1e17;
const double inf = 1e20;
const double PI = acos(-1.0);
const double eps = 1e-8;
const int maxn = 1e4 + 5;
const int maxm = 2e4 + 10;
const LL mod = 10007;
const int dr[] = {-1, 1, 0, 0, 1, 1, -1, -1};
const int dc[] = {0, 0, 1, -1, 1, -1, 1, -1};
const char *de[] = {"0000", "0001", "0010", "0011", "0100", "0101", "0110", "0111", "1000", "1001", "1010", "1011", "1100", "1101", "1110", "1111"};
int n, m;
const int mon[] = {0, 31, 28, 31, 30, 31, 30, 31, 31, 30, 31, 30, 31};
const int monn[] = {0, 31, 29, 31, 30, 31, 30, 31, 31, 30, 31, 30, 31};
inline bool is_in(int r, int c) {
  return r >= 0 && r < n && c >= 0 && c < m;
}

int a[maxn], len[maxn];
bool vis[maxn];
int prime[maxn], mu[maxn];

void Moblus(){
  mu[1] = 1;
  int tot = 0;
  for(int i = 2; i < maxn; ++i){
    if(!vis[i])  prime[tot++] = i, mu[i] = -1;
    for(int j = 0; j < tot; ++j){
      int t = i * prime[j];
      if(t >= maxn)  break;
      vis[t] = 1;
      if(i % prime[j] == 0)  break;
      mu[t] = -mu[i];
    }
  }
}

int f[maxn];

int main(){
  Moblus();
  while(scanf("%d", &n) == 1){
    ms(a, 0);  ms(len, 0);  ms(f, 0);
    for(int i = 0; i < n; ++i){
      int x;  scanf("%d", &x);
      ++a[x];
    }

    for(int i = 1; i < maxn; ++i)
      for(int j = i; j < maxn; j += i)
        len[i] += a[j];
    for(int i = 1; i < maxn; ++i)
      for(int j = i, cnt = 1; j < maxn; j += i, ++cnt)
        f[i] += mu[cnt] * sqr(len[j]);
    LL ans = 0;
    for(int i = 2; i < maxn; ++i)
      ans = (ans + i * (i-1) * (LL)f[i]) % mod;
    printf("%lld\n", ans);
  }
  return 0;
}