[Alg] 二叉树的非递归遍历

1. 非递归遍历二叉树算法 (使用stack)

以非递归方式对二叉树进行遍历的算法需要借助一个栈来存放访问过得节点。

(1) 前序遍历

从整棵树的根节点开始，对于任意节点V，访问节点V并将节点V入栈，并判断节点V的左子节点L是否为空。若L不为空，则将L置为当前节点V；若L为空，则取出栈顶节点，并将栈顶结点的右子节点置为当前节点V。重复上述操作，直到当前节点V为空并且栈为空，遍历结束。

(2) 中序遍历

从整棵树的根节点开始，对于任意节点V，判断其左子节点L是否为空。若L不为空，则将V入栈并将L置为当前节点V；若L为空，则取出栈顶节点并访问该栈顶节点，然后将其右子节点置为当前节点V。重复上述操作，直到当前节点V为空节点且栈为空，遍历结束。

(3) 后序遍历

首先将整颗二叉树的根节点入栈。取栈顶节点V，若V不存在左子节点和右子节点，或V存在左子节点或右子节点但其左子节点和右子节点都被访问过了，则访问节点V，并将V从栈中弹出。若非上述两种情况，则将V的右子节点和左子节点(注意先右后左，这样出栈时才能先左后右)依次入栈。重复上述操作，直到栈为空，遍历结束。

2. 二叉树递归与非递归遍历代码

 #include "stdafx.h"
 #include <stdio.h>
 #include <stdlib.h>
 #include <string.h>

 #define Stack_increment 20
 #define Stack_Size 100  

 typedef struct  Tree
 {
     char data;
     struct Tree *lchild;
     struct Tree *rchild;
 }Node;

 Node* createBinaryTree()
 {
     Node *root;
     char ch;
     scanf("%c", &ch);

     if (ch == '#')
     {
         root = NULL;
     }
     else
     {
         root = (Node *)malloc(sizeof(Node));
         root -> data = ch;
         root -> lchild = createBinaryTree();
         root -> rchild = createBinaryTree();
     }

     return root;
 }

 typedef struct
 {
     int top;
     Node* arr[Stack_Size];
 }Stacktree;

 void InitStack(Stacktree *S)
 {
     S->top = 0;
 }

 void Push(Stacktree* S, Node* x)
 {
     int top1 = S -> top;
     if (x -> data == '#')
     {
         return;
     }
     else
     {
         S -> arr[top1++] = x;
         S -> top++;
     }
 }

 int Pop(Stacktree *S)
 {
     int top = S -> top;
     if (S->top == 0)
     {
         return 0;
     }
     else
     {
         --(S->top);
         return 1;
     }
 }

 Node* GetTop(Stacktree *S)
 {
     int top1 = S -> top;
     Node*p;
     p = S -> arr[top1--];
     return p;
 }

 Node* GetTop1(Stacktree *S)
 {
     int top1 = S -> top;
     Node*p;
     top1--;
     p = S -> arr[top1];
     return p;
 }

 int IsEmpty(Stacktree *S)
 {
     return(S->top == 0 ? 1 : 0);
 }

 void preorderRecursive(Node *p )
 {
     if (p != NULL)
     {
         printf("%c ", p -> data);
         preorderRecursive(p -> lchild);
         preorderRecursive(p -> rchild);
     }
 }

 void inorderRecursive(Node *p )
 {
     if (p != NULL)
     {
         inorderRecursive(p -> lchild);
         printf("%c ", p -> data);
         inorderRecursive(p -> rchild);
     }
 }

 void postorderRecursive(Node *p )
 {
     if (p != NULL)
     {
         postorderRecursive(p -> lchild);
         postorderRecursive(p -> rchild);
         printf("%c ", p -> data);
     }
 }

 void preordernotRecursive(Node *p)
 {
     if(p)
     {
         Stacktree stree ;
         InitStack(&stree);
         Node *root = p;
         while(root != NULL || !IsEmpty(&stree))
         {
             while(root != NULL)
             {
                 printf("%c  ", root->data);
                 Push(&stree, root);
                 root = root -> lchild;
             }

             if(!IsEmpty(&stree))
             {
                 Pop(&stree);
                 root = GetTop(&stree);
                 root = root -> rchild;
             }
         }
     }
 }

 void inordernotRecursive(Node *p)
 {
     if(p)
     {
         Stacktree stree;
         InitStack(&stree);
         Node *root = p;
         while(root != NULL || !IsEmpty(&stree))
         {
             while(root != NULL)
             {
                 Push(&stree, root);
                 root = root -> lchild;
             }

             if(!IsEmpty(&stree))
             {
                 Pop(&stree);
                 root = GetTop(&stree);
                 printf("%c  ", root -> data);
                 root = root -> rchild;
             }
         }
     }
 }

 void postordernotRecursive(Node *p)
 {
     Stacktree stree;
     InitStack(&stree);

     Node *root;
     Node *pre = NULL;    

     Push(&stree, p);

     while (!IsEmpty(&stree))
     {
         root = GetTop1(&stree);

         if ((root -> lchild == NULL && root -> rchild == NULL) || (pre != NULL && (pre == root -> lchild || pre == root -> rchild)))
         {
             printf("%c ", root -> data);
             Pop(&stree);
             pre = root;
         }

         else
         {
             if (root -> rchild != NULL)
             {
                 Push(&stree, root -> rchild);
             }

             if (root -> lchild != NULL)
             {
                 Push(&stree, root -> lchild);
             }
         }

     }
 }

 void main()
 {

     printf("请输入二叉树，'#'为空\n");
     Node *root = createBinaryTree();

     printf("\n递归先序遍历:\n");
     preorderRecursive(root);

     printf("\n递归中序遍历:\n");
     inorderRecursive(root);

     printf("\n递归后序遍历:\n");
     postorderRecursive(root);

     printf("\n非递归先序遍历\n");
     preordernotRecursive(root);

     printf("\n非递归中序遍历\n");
     inordernotRecursive(root);

     printf("\n非递归后序遍历\n");
     postordernotRecursive(root);

     getchar();
     getchar();
 }

(代码中的top是栈顶元素的上一位的index，不是栈顶元素的index～)

input:

ABC##D##E##

output:

递归先序遍历:

A B C D E

递归中序遍历:

C B D A E

递归后序遍历:

C D B E A

非递归先序遍历:

A B C D E

非递归中序遍历:

C B D A E

非递归后序遍历:

C D B E A

3. Morris Traversal (遍历二叉树无需stack)

Morris Traversal 是一种非递归无需栈仅在常量空间复杂度的条件下即可实现二叉树遍历的一种很巧妙的方法。该方法的实现需要构造一种新型的树结构，Threaded Binary Tree.

3.1 Threaded Binary Tree 定义

Threaded binary tree: A binary tree is threaded by making all right child pointers that would normally be null point to the inorder successor of the node (if it exists), and all left child pointers that would normally be null point to the inorder predecessor of the node. ~WIkipedia

Threaded binary tree 的构造相当于将所有原本为空的右子节点指向了中序遍历的该点的后续节点，把所有原本为空的左子节点都指向了中序遍历的该点前序节点。如图1所示。

那么通过这种方式，对于当前节点cur, 若其右子树为空，(cur -> right = NULL)，那么通过沿着其pre指针，即可返回其根节点继续遍历。

比如对于图1中的节点A，其右孩子为空，则说明以A为根节点的子树遍历完成，沿着其pre指针可以回到A的根节点B，继续遍历。这里的pre指针相当于保存了当前节点的回溯的位置信息。

 

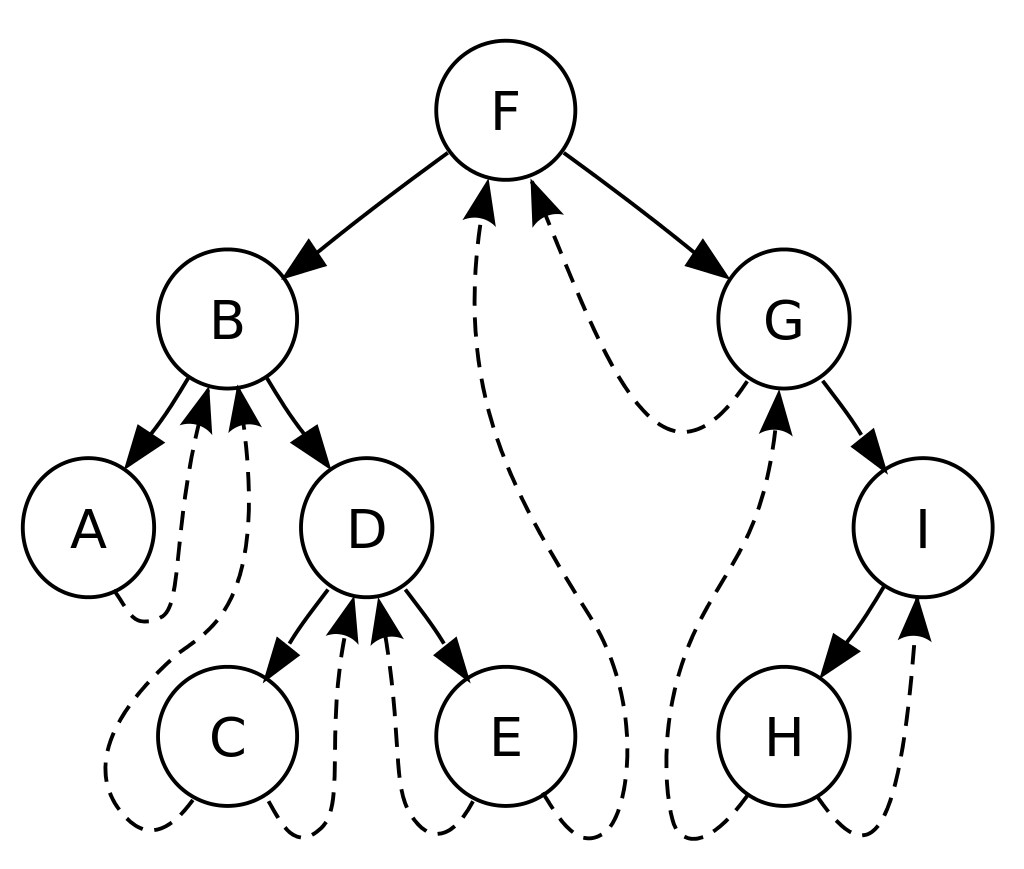
图1. Threaded binary tree         图2. Threaded tree构造及遍历算法图示

3.2 Threaded Binary Tree 算法实现

3.2.1 算法描述

1. 初始化指针cur = root

2. while (cur != NULL)

2.1 if cur -> left == NULL

a) print(cur -> val)

b) cur = cur -> right

2.2 else if cur -> left != NULL

将pre 指向cur 的左子树中的 最右子节点 (并保证不指回cur)

2.2.1 if pre -> right == NULL

a) pre -> right = cur

b) cur = cur -> left

2.2.2 else if pre -> right != NULL (说明pre -> right是用于指回cur节点的指针)

a) 将pre -> right 置空

　　　　　 b) print(cur -> val)

　　　　     c) cur = cur -> right

3.2.2 代码实现 (中序)

 # include <bits/stdc++.h>
 using namespace std;

 struct TreeNode
 {
     int val;
     struct TreeNode *right;
     struct TreeNode *left;
     TreeNode(int x): val(x), left(NULL), right(NULL) {}
 };

 vector<int> inorderTraversal(TreeNode *root)
 {
     vector<int> res;
     if(!root) return res;
     TreeNode *cur, *pre;
     cur = root;

     while(cur)
     {
         if(cur -> left == NULL)
         {
             res.push_back(cur -> val);
             cur = cur -> right;
         }

         else if(cur -> left != NULL)
         {
             pre = cur -> left;
             while(pre -> right && pre -> right != cur) pre = pre -> right;
             if(pre -> right == NULL)
             {
                 pre -> right = cur;
                 cur = cur -> left;
             }
             else if(pre -> right != NULL)
             {
                 pre -> right = NULL;
                 res.push_back(cur -> val);
                 cur = cur -> right;
             }
         }
     }
     return res;
 }

 int main()
 {
     vector<int> res;
     TreeNode *node1 = new TreeNode();
     TreeNode *node2 = new TreeNode();
     TreeNode *node3 = new TreeNode();
     TreeNode *node4 = new TreeNode();
     node1 -> left = node2;
     node2 -> left = node3;
     node3 -> right = node4;
     inorderTraversal(node1);
     res = inorderTraversal(node1);
     vector<int>::iterator it;
     for(it = res.begin(); it != res.end(); ++it)
     {
         cout << *it << " ";
     }
     cout << endl;
     delete node1; delete node2;
     delete node3; delete node4;
     return ;
 }

 // 3 4 2 1

参考：

1. 以先序、中序、后序的方式递归非递归遍历二叉树：https://blog.csdn.net/asd20172016/article/details/80786186

2. Morris Traversal: [LeetCode] Binary Tree Inorder Traversal 二叉树的中序遍历: https://www.cnblogs.com/grandyang/p/4297300.html

3. [LeetCode] Recover Binary Search Tree 复原二叉搜索树: https://www.cnblogs.com/grandyang/p/4298069.html

4. Wikipedia: Threaded binary tree: https://en.wikipedia.org/wiki/Threaded_binary_tree