数据结构之AVL

简介：

一棵AVL树有如下必要条件：

　　条件一：它必须是二叉查找树。（左<根<右）

　　

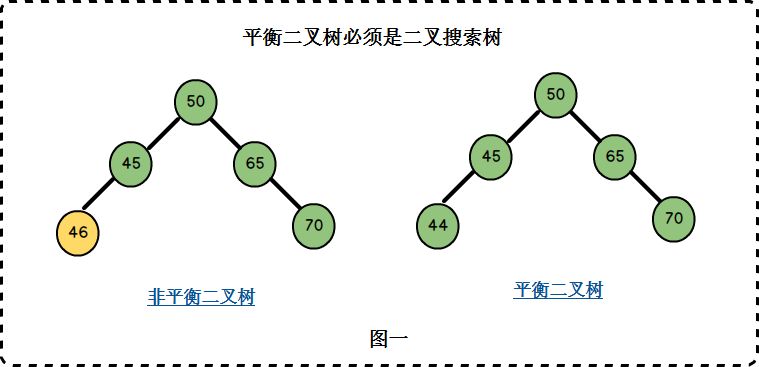
　　条件二：每个节点的左子树和右子树的高度差至多为1。

　　

AVL相关概念：

平衡因子：将二叉树上节点的左子树高度减去右子树高度的值称为该节点的平衡因子BF(Balance Factor)。
　　　　　　对于平衡二叉树，BF的取值范围为[-1,1]。如果发现某个节点的BF值不在此范围，则需要对树进行调整。

最小不平衡子树：距离插入节点最近的，且平衡因子的绝对值大于1的节点为根的子树。

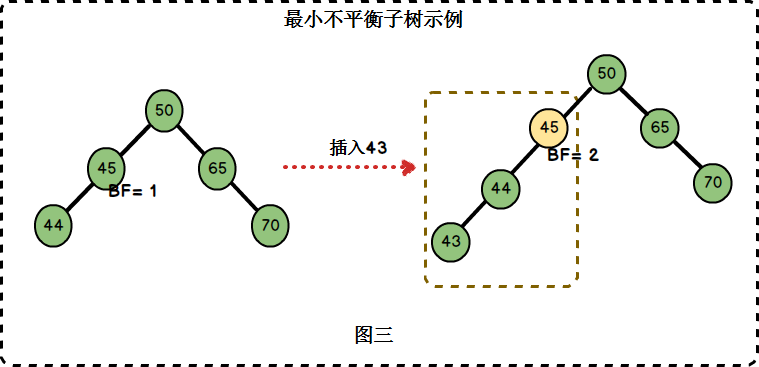
在图三中，左边二叉树的节点45的BF = 1，插入节点43后，节点45的BF = 2。节点45是距离插入点43最近的BF不在[-1,1]范围内的节点，因此以节点45为根的子树为最小不平衡子树。

AVL树失衡调整

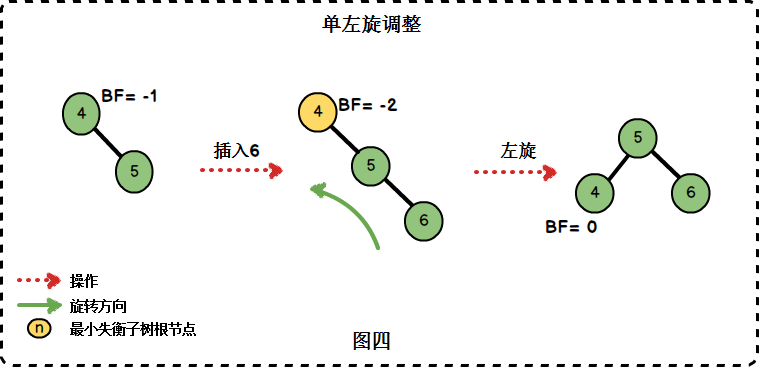
单左旋调整：

1. 参数proot为最小失衡子树的根节点，在图四中为节点4
2. 若节点5有左子树，则该左子树成为节点4的右子树
3. 节点4成为节点5的左子树
4. 最后更新节点的高度值

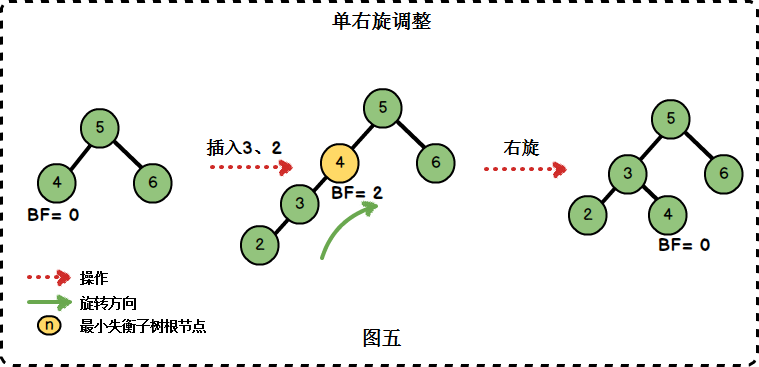
右单旋转：

1. 参数proot为最小失衡子树的根节点，在图四中为节点4
2. 若节点3有右子树，则该右子树成为节点4的左子树
3. 节点4成为节点3的左子树
4. 调整节点的高度值

　　

先左旋后右旋（或者先右旋后左旋）都是先对子节点旋转变成最小失衡节点的单右旋（或单右旋）。

删除节点也可能导致AVL树的失衡，实际上删除节点和插入节点是一种互逆的操作：

1. 删除右子树的节点导致AVL树失衡时，相当于在左子树插入节点导致AVL树失衡，即情况情况二或情况四。
2. 删除左子树的节点导致AVL树失衡时，相当于在右子树插入节点导致AVL树失衡，即情况情况一或情况三。

删除节点时，如果节点同时拥有左子树和右子树，则在高度教低的子树上选择最大（或最小）元素进行替换，这样能保证替换后不会再出现失衡的现象。

参考文章：

https://www.cnblogs.com/QG-whz/p/5167238.html