听课笔记--DP--最大子矩阵和

---

最大子矩阵问题

给定一个n*n(0<n<=120)的矩阵，

矩阵内元素有正有负，

请找到此矩阵的内部元素和最大的子矩阵

样例输入：

4

0 -2 -7  0

9  2 -6  2

-4  1 -4  1

-1  8  0 -2

样例输出：

15

---

• 方法一：

  用二维前缀和维护然后一个个点遍历；

  时间复杂度：O（N4）；

• 方法二：

  DP

  先请明白这道题：

  最大子段和

  嗯？这不是一维的吗。和这道题有什么关系？

  请看这张图：

  

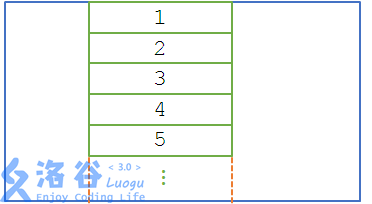
     这样就不难看出，我们只要枚举区间的左端点l和右端点r；
  
     同时用维护的二维前缀和求出每一段1,2,3,4,的值
  
     然后竖着来一遍最大字段和（O（N））就好了
  
     时间复杂度：O（N3）
  

---

代码：

#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <algorithm>
using namespace std;
const int maxn=150;
int a[maxn][maxn];
int sum[maxn][maxn];
int line[maxn],c[maxn];
int l,r;
int n;
int solve()
{
	int minx=min(0,line[1]),maxx=line[1];//
	for(int i=2;i<=n;i++)
	{
		maxx=max(maxx,c[i]-minx);
		minx=min(minx,c[i]);
	}
	return maxx;
}
int main()
{
	int ans=-99999;
	cin>>n;
	for(int i=1;i<=n;i++)
	{
		for(int j=1;j<=n;j++)
		{
		cin>>a[i][j];
		sum[i][j]=sum[i][j-1]+a[i][j];
	    }
	}
	for(r=1;r<=n;r++)
	{
		for(l=1;l<=r;l++)
		{
			for(int i=1;i<=n;i++)
			{
			line[i]=sum[i][r]-sum[i][l]+a[i][l];
			c[i]=c[i-1]+line[i];
		    }
		     ans=max(solve(),ans);
		     memset(c,0,sizeof(c));
		     memset(line,0,sizeof(line));
		}

	}
	cout<<ans<<endl;
	return 0;
}