HDU 5734 Acperience ( 数学公式推导、一元二次方程 )

题目链接

题意 : 给出 n 维向量 W、要你构造一个 n 维向量 B = ( b1、b2、b3 ..... ) ( bi ∈ { +1, -1 } ) 、然后求出对于一个常数 α > 0 使得 || W - αB ||^2 尽量小

分析 :

将 || W - αB || ^ 2 进行化简、如下

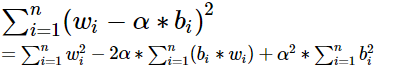
未知数是 α

不难看出这是一个一元二次方程 Ax^2 + Bx + C

而根据实际的贪心选择

当 wi > 0 时、有 bi < 0

当 wi < 0 时、有 bi > 0

那么上述方程的 A、B、C 都可以确定并求出且 A > 0

那么根据公式法、此方程有最小值 (4AC - B^2) / (4A)

直接求就行了

#include<bits/stdc++.h>
#define LL long long
#define ULL unsigned long long

#define scl(i) scanf("%lld", &i)
#define scll(i, j) scanf("%lld %lld", &i, &j)
#define sclll(i, j, k) scanf("%lld %lld %lld", &i, &j, &k)
#define scllll(i, j, k, l) scanf("%lld %lld %lld %lld", &i, &j, &k, &l)

#define scs(i) scanf("%s", i)
#define sci(i) scanf("%d", &i)
#define scd(i) scanf("%lf", &i)
#define scIl(i) scanf("%I64d", &i)
#define scii(i, j) scanf("%d %d", &i, &j)
#define scdd(i, j) scanf("%lf %lf", &i, &j)
#define scIll(i, j) scanf("%I64d %I64d", &i, &j)
#define sciii(i, j, k) scanf("%d %d %d", &i, &j, &k)
#define scddd(i, j, k) scanf("%lf %lf %lf", &i, &j, &k)
#define scIlll(i, j, k) scanf("%I64d %I64d %I64d", &i, &j, &k)
#define sciiii(i, j, k, l) scanf("%d %d %d %d", &i, &j, &k, &l)
#define scdddd(i, j, k, l) scanf("%lf %lf %lf %lf", &i, &j, &k, &l)
#define scIllll(i, j, k, l) scanf("%I64d %I64d %I64d %I64d", &i, &j, &k, &l)

#define lson l, m, rt<<1
#define rson m+1, r, rt<<1|1
#define lowbit(i) (i & (-i))
#define mem(i, j) memset(i, j, sizeof(i))

#define fir first
#define sec second
#define VI vector<int>
#define ins(i) insert(i)
#define pb(i) push_back(i)
#define pii pair<int, int>
#define VL vector<long long>
#define mk(i, j) make_pair(i, j)
#define all(i) i.begin(), i.end()
#define pll pair<long long, long long>

#define _TIME 0
#define _INPUT 0
#define _OUTPUT 0
clock_t START, END;
void __stTIME();
void __enTIME();
void __IOPUT();
using namespace std;

;

LL w[maxn], b[maxn];
int n;

int main(void){__stTIME();__IOPUT();

    printf("%d", b);

    int nCase;
    sci(nCase);
    while(nCase--){
        sci(n);

        ; i<=n; i++){
            scl(w[i]);
            ) b[i] = 1LL;
            else b[i] = - 1LL;
        }

        LL C = ;
        ; i<=n; i++)
            C += (w[i] * w[i]);

        LL B = ;
        ; i<=n; i++)
            B += (w[i] * b[i]);
        B *= (- 2LL);

        LL A = ;
        ; i<=n; i++)
            A += (b[i] * b[i]);

        LL p = ( * A * C - B * B);
        LL q =  * A;

        LL GCD = __gcd(p, q);

        p /= GCD;
        q /= GCD;

        printf("%lld/%lld\n", p, q);
    }

__enTIME();;}

void __stTIME()
{
    #if _TIME
        START = clock();
    #endif
}

void __enTIME()
{
    #if _TIME
        END = clock();
        cerr<<"execute time = "<<(double)(END-START)/CLOCKS_PER_SEC<<endl;
    #endif
}

void __IOPUT()
{
    #if _INPUT
        freopen("in.txt", "r", stdin);
    #endif
    #if _OUTPUT
        freopen("out.txt", "w", stdout);
    #endif
}