poj 3352Road Construction（无向双连通分量的分解）

 /*
    题意：给定一个连通的无向图G，至少要添加几条边，才能使其变为强连通图（指的是边强联通）。
    思路：利用tarjan算法找出所有的双联通分量！然后根据low[]值的不同将双联通分量
    进行缩点，最后图形会变成一棵树！也就是添加至少多少条边使一棵树变成强联通图！
    

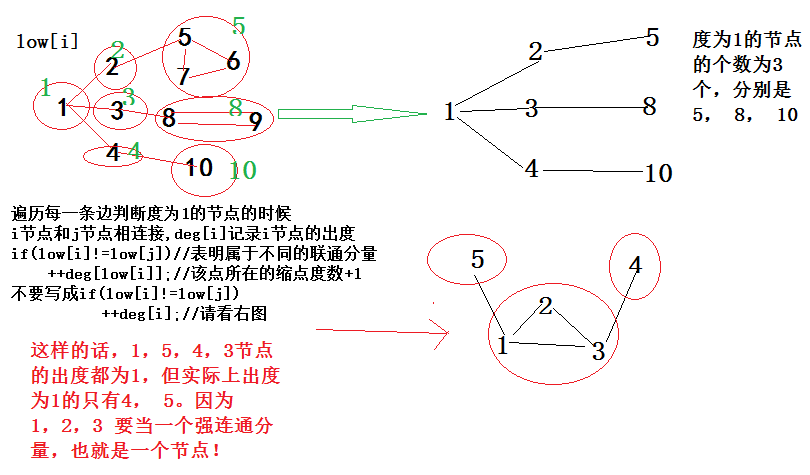
    知识点：若要使得任意一棵树，在增加若干条边后，变成一个双连通图，那么
            至少增加的边数 =（ 这棵树总度数为1的结点数 + 1 ）/ 2 

 */
 #include<iostream>
 #include<cstring>
 #include<cstdio>
 #include<algorithm>
 #include<vector>
 #define N 1005
 using namespace std;
 vector<int>g[N];
 int low[N], pre[N];
 int deg[N];
 int n, m;
 int cnt;
 int dfsClock;
 void dfs(int u, int fa){
     low[u]=pre[u]=++dfsClock;
     int len=g[u].size();
     for(int i=; i<len; ++i){
         int v=g[u][i];
         if(!pre[v]){
            dfs(v, u);
            low[u]=min(low[u], low[v]);
         }
         else if(pre[v] < pre[u] && fa!=v)
            low[u]=min(pre[v], low[u]);
     }
 }

 int main(){
     while(scanf("%d%d", &n, &m)!=EOF){
         memset(pre, , sizeof(pre));
         memset(deg, , sizeof(deg));
         while(m--){
            int u, v;
            scanf("%d%d", &u, &v);
            g[u].push_back(v);
            g[v].push_back(u);
         }
         cnt=;
         dfsClock=;
         dfs(, -);
         for(int i=; i<=n; ++i){
            int len=g[i].size();
            for(int j=; j<len; ++j){
                   int v=g[i][j];
                   if(low[i]!=low[v])
                    ++deg[low[i]];
            }
         }
         for(int i=; i<=n; ++i)
             if(deg[i]==)
                ++cnt;
         printf("%d\n", (cnt+)/);
         for(int i=; i<=n; ++i)
            g[i].clear();
     }
     return ;
 }