SLAM中的变换（旋转与位移）表示方法

１、旋转矩阵

注：旋转矩阵标题下涉及到的SLAM均不包含位移。

根据同一点P在不同坐标系下e(e₁,e₂,e₃)e'(e₁',e₂',e₃')的坐标a(a₁,a₂,a₃)a'(a₁',a₂',a₃')有如下等式成立：

 

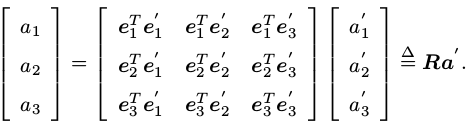
即a = e^Te'a‘,其中e^Te'设为R为旋转矩阵，即a = Ra‘,由此便得到P在e'坐标系下到e坐标系下的坐标变换。

在SLAM中一般a'为相机坐标系下坐标P_c，a为世界坐标系下坐标P_w。则有P_w = RP_c

其中R = e^Te'  →  eR = e'

如果把R分成三个列向量，则每个列向量即为e’坐标系的基在e坐标系下的坐标。

与此对应SLAM中即为相机坐标系下的坐标轴在世界坐标系下的坐标。

(a₁₁,a₂₁,a₃₁)即为基e₁'在e坐标系下的坐标（e'坐标系的另两个基e_２'，e_３'亦如此）。

与此对应的slam中即为相机坐标系下ｘ坐标轴在世界坐标系下的坐标。

SLAM中这里的R一般被称为相机的姿态（不是位姿，不包含平移）。