Willem, Chtholly and Seniorious

Willem, Chtholly and Seniorious

https://codeforces.com/contest/897/problem/E

time limit per test

2 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

— Willem...

— What's the matter?

— It seems that there's something wrong with Seniorious...

— I'll have a look...

Seniorious is made by linking special talismans in particular order.

After over 500 years, the carillon is now in bad condition, so Willem decides to examine it thoroughly.

Seniorious has n pieces of talisman. Willem puts them in a line, the i-th of which is an integer ai.

In order to maintain it, Willem needs to perform m operations.

There are four types of operations:

• 1 l r x: For each i such that l ≤ i ≤ r, assign ai + x to ai.
• 2 l r x: For each i such that l ≤ i ≤ r, assign x to ai.
• 3 l r x: Print the x-th smallest number in the index range [l, r], i.e. the element at the x-th position if all the elements ai such that l ≤ i ≤ r are taken and sorted into an array of non-decreasing integers. It's guaranteed that 1 ≤ x ≤ r - l + 1.
• 4 l r x y: Print the sum of the x-th power of ai such that l ≤ i ≤ r, modulo y, i.e. .

Input

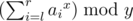The only line contains four integers n, m, seed, vmax (1 ≤ n, m ≤ 105, 0 ≤ seed < 109 + 7, 1 ≤ vmax ≤ 109).

The initial values and operations are generated using following pseudo code:

def rnd():

    ret = seed
    seed = (seed * 7 + 13) mod 1000000007
    return ret

for i = 1 to n:

    a[i] = (rnd() mod vmax) + 1

for i = 1 to m:

    op = (rnd() mod 4) + 1
    l = (rnd() mod n) + 1
    r = (rnd() mod n) + 1

    if (l > r): 
         swap(l, r)

    if (op == 3):
        x = (rnd() mod (r - l + 1)) + 1
    else:
        x = (rnd() mod vmax) + 1

    if (op == 4):
        y = (rnd() mod vmax) + 1

Here op is the type of the operation mentioned in the legend.

Output

For each operation of types 3 or 4, output a line containing the answer.

Examples

input

Copy

10 10 7 9

output

Copy

2
1
0
3

input

Copy

10 10 9 9

output

Copy

1
1
3
3

Note

In the first example, the initial array is {8, 9, 7, 2, 3, 1, 5, 6, 4, 8}.

The operations are:

• 2 6 7 9
• 1 3 10 8
• 4 4 6 2 4
• 1 4 5 8
• 2 1 7 1
• 4 7 9 4 4
• 1 2 7 9
• 4 5 8 1 1
• 2 5 7 5
• 4 3 10 8 5

ODT模板题

参考博客：https://blog.csdn.net/niiick/article/details/83062256

 #include<bits/stdc++.h>
 using namespace std;
 #define lson l,mid,rt<<1
 #define rson mid+1,r,rt<<1|1
 #define IT set<node>::iterator
 #define sqr(x) ((x)*(x))
 #define pb push_back
 #define eb emplace_back
 #define maxn 100005
 #define eps 1e-8
 #define pi acos(-1.0)
 #define rep(k,i,j) for(int k=i;k<j;k++)
 typedef long long ll;
 typedef pair<int,int> pii;
 typedef pair<ll,ll>pll;
 typedef pair<ll,int> pli;
 typedef pair<pair<int,string>,pii> ppp;
 typedef unsigned long long ull;
 const long long MOD=1e9+;
 const double oula=0.57721566490153286060651209;
 using namespace std;

 struct node{
     int l,r;
     mutable ll val;
     node(int L,int R=-,ll V=):l(L),r(R),val(V){}
     bool operator<(const node& t)const {
         return l<t.l;
     }
 };
 set<node>se;

 ll ksm(ll a,ll b,ll mod){
     ll ans=;
     a%=mod;
     while(b){
         if(b&){
             ans=(ans*a)%mod;
         }
         b>>=;
         a=(a*a)%mod;
     }
     return ans;
 }

 IT split(int pos){
     IT it=se.lower_bound(node(pos));
     if(it!=se.end()&&it->l==pos) return it;
     it--;
     int L=it->l,R=it->r;
     ll V=it->val;
     se.erase(it);
     se.insert(node(L,pos-,V));
     return se.insert(node(pos,R,V)).first;///返回L==pos的迭代器
 }

 void assign(int l,int r,ll v){
     IT itr=split(r+),itl=split(l);
     se.erase(itl,itr);///左闭右开
     se.insert(node(l,r,v));
 }

 void add(int l,int r,ll v){
     IT itr=split(r+);
     for(IT itl=split(l);itl!=itr;itl++){
         itl->val+=v;
     }
 }

 ll Rank(int l,int r,int v){
     IT itr=split(r+);
     vector<pli>tmp;
     for(IT itl=split(l);itl!=itr;itl++){
         tmp.pb({itl->val,itl->r-itl->l+});
     }
     sort(tmp.begin(),tmp.end());
     for(int i=;i<tmp.size();i++){
         v-=tmp[i].second;
         if(v<=){
             return tmp[i].first;
         }
     }
 }

 ll query(int l,int r,ll x,ll y){
     IT itr=split(r+);
     ll ans=;
     for(IT itl=split(l);itl!=itr;itl++){
         ans=(ans+((ksm(itl->val,x,y)*(itl->r-itl->l+))%y))%y;
     }
     return ans;
 }

 ll n,m,seed,vmax;

 ll rnd(){
     ll ans=seed;
     seed=(seed*+)%MOD;
     return ans;
 }

 int main(){
     std::ios::sync_with_stdio(false);

     cin>>n>>m>>seed>>vmax;
     ll x,y;
     for(int i=;i<=n;i++){
         x=(rnd()%vmax)+;
         se.insert(node(i,i,x));
     }
     int opt,L,R;
     for(int i=;i<=m;i++){
         opt=(rnd()%)+;
         L=(rnd()%n)+;
         R=(rnd()%n)+;
         if(L>R) swap(L,R);
         if(opt==){
             x=(rnd()%(R-L+))+;
         }
         else{
             x=(rnd()%vmax)+;
         }
         if(opt==){
             y=(rnd()%vmax)+;
         }
         if(opt==){
             add(L,R,x);
         }
         else if(opt==){
             assign(L,R,x);
         }
         else if(opt==){
             cout<<Rank(L,R,x)<<endl;
         }
         else{
             cout<<query(L,R,x,y)<<endl;
         }
     }
 }