[codevs1380]没有上司的舞会（[BZOJ2060][Usaco2010 Nov]Visiting Cows 拜访奶牛）

[codevs1380]没有上司的舞会

试题描述

Ural大学有N个职员，编号为1~N。他们有从属关系，也就是说他们的关系就像一棵以校长为根的树，父结点就是子结点的直接上司。每个职员有一个快乐指数。现在有个周年庆宴会，要求与会职员的快乐指数最大。但是，没有职员愿和直接上司一起与会。

输入

第一行一个整数N。(1<=N<=6000)
接下来N行，第i+1行表示i号职员的快乐指数Ri。(-128<=Ri<=127)
接下来N-1行，每行输入一对整数L,K。表示K是L的直接上司。
最后一行输入0,0。

输出

输出最大的快乐指数。

输入示例

输出示例

数据规模及约定

见“输入”

题解

我来刷水了！

把每个人看成一个节点。设 f[0][i] 表示对于子树 i，不选择 i 节点能够得到的最大值；f[1][i] 表示选择 i 节点能够得到的最大值。那么，

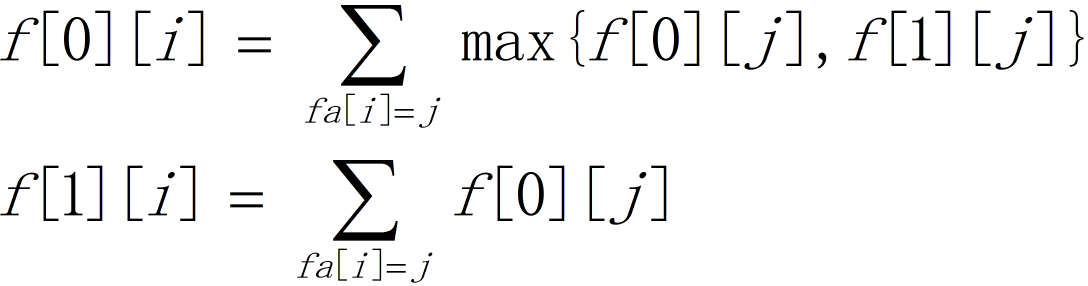
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cmath>
#include <stack>
#include <vector>
#include <queue>
#include <cstring>
#include <string>
#include <map>
#include <set>
using namespace std;

const int BufferSize = 1 << 16;
char buffer[BufferSize], *Head, *Tail;
inline char Getchar() {
    if(Head == Tail) {
        int l = fread(buffer, 1, BufferSize, stdin);
        Tail = (Head = buffer) + l;
    }
    return *Head++;
}
int read() {
    int x = 0, f = 1; char c = Getchar();
    while(!isdigit(c)){ if(c == '-') f = -1; c = Getchar(); }
    while(isdigit(c)){ x = x * 10 + c - '0'; c = Getchar(); }
    return x * f;
}

#define maxn 6010
#define maxm 12010
int n, m, head[maxn], next[maxm], to[maxm], val[maxn];

void AddEdge(int a, int b) {
	to[++m] = b; next[m] = head[a]; head[a] = m;
	swap(a, b);
	to[++m] = b; next[m] = head[a]; head[a] = m;
	return ;
}

int f[2][maxn];
void dp(int u, int fa) {
	f[0][u] = 0; f[1][u] = val[u];
	for(int e = head[u]; e; e = next[e]) if(to[e] != fa) {
		dp(to[e], u);
		f[0][u] += max(f[0][to[e]], f[1][to[e]]);
		f[1][u] += f[0][to[e]];
	}
	return ;
}

int main() {
	n = read();
	for(int i = 1; i <= n; i++) val[i] = read();
	for(int i = 1; i < n; i++) {
		int a = read(), b = read();
		AddEdge(a, b);
	}
	read(); read();

	dp(1, 0);

	printf("%d\n", max(f[0][1], f[1][1]));

	return 0;
}

双倍经验：BZOJ2060，改改输入。