柯尔莫可洛夫-斯米洛夫检验（Kolmogorov–Smirnov test，K-S test）

柯尔莫哥洛夫-斯米尔诺夫检验（Колмогоров-Смирнов检验）基于累计分布函数，用以检验两个经验分布是否不同或一个经验分布与另一个理想分布是否不同。

在进行cumulative probability统计(如下图)的时候，你怎么知道组之间是否有显著性差异？有人首先想到单因素方差分析或双尾检验（2 tailed TEST）。其实这些是不准确的，最好采用Kolmogorov-Smirnov test（柯尔莫诺夫-斯米尔诺夫检验）来分析变量是否符合某种分布或比较两组之间有无显著性差异。

Kolmogorov-Smirnov test原理：寻找最大距离（Distance）， 所以常简称为D法。 适用于大样本。 KS test checks if two independent distributions are similar or different, by generating cumulative probability plots for two distributions and finding the distance along the y-axis for a given x values between the two curves. From all the distances calculated for each x value, the maximum distance is searched.

如何分析结果呢？This maximum distance or maximum difference is then plugged into KS probability function to calculate the probability value.  The lower the probability value is the less likely the two distributions are similar.  Conversely, the higher or more close to 1 the value is the more similar the two distributions are.极端情况：如果P值为１的话，说明两给数据基本相同，如果P值无限接近０，说明两组数据差异性极大。

 

有一个网站可以进行在线的统计，你只需要输入数据就可以了。地址如下：http://www.physics.csbsju.edu/stats/KS-test.n.plot_form.html

当然还有更多的软件支持这个统计，如SPSS,SAS,MiniAnalysis,Clampfit10

根据软件统计出来后给出的结果决定有没有显著性差异，如果D _max值>D _0.05。则认为有显著性差异。D _0.05的经验算法：1.36/SQRT(N) 其中SQRT为平方要，N为样本数。D _0.0１经验算法1.64/SQRT(N) 。当然最准确的办法还是去查KS检定表。不过大多数软件如CLAMPFIT,MINIANALYSIS统计出来的结果都是直接有P值。根据这个值（alpha=0.05）就可以断定有没有差异了。

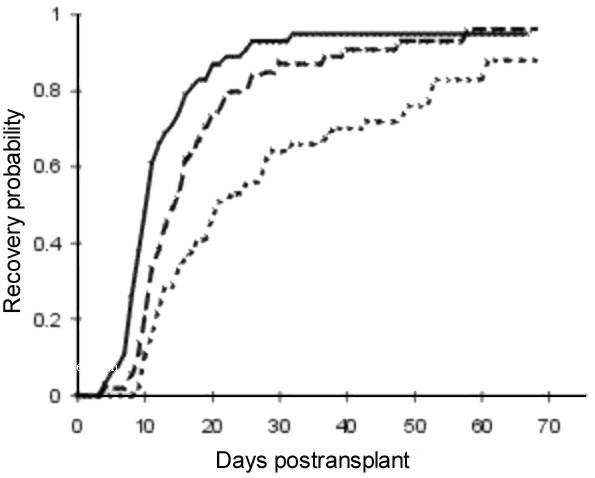
在统计学中，柯尔莫可洛夫-斯米洛夫检验基于累计分布函数，用以检验两个经验分布是否不同或一个经验分布与另一个理想分布是否不同。

在进行累计概率（cumulative probability）统计的时候，你怎么知道组之间是否有显著性差异？有人首先想到单因素方差分析或双尾检验（2 tailedTEST）。其实这些是不准确的，最好采用Kolmogorov-Smirnov test（柯尔莫诺夫-斯米尔诺夫检验）来分析变量是否符合某种分布或比较两组之间有无显著性差异。

分类：

1、Single sample Kolmogorov-Smirnov goodness-of-fit hypothesis test.

采用柯尔莫诺夫-斯米尔诺夫检验来分析变量是否符合某种分布，可以检验的分布有正态分布、均匀分布、Poission分布和指数分布。指令如下：

>> H = KSTEST(X,CDF,ALPHA,TAIL) % X为待检测样本，CDF可选：如果空缺，则默认为检测标准正态分布；

如果填写两列的矩阵，第一列是x的可能的值，第二列是相应的假设累计概率分布函数的值G(x)。ALPHA是显著性水平（默认0.05）。TAIL是表示检验的类型（默认unequal,不平衡）。还有larger，smaller可以选择。

如果，H=1 则否定无效假设； H=0，不否定无效假设（在alpha水平上）

例如，

x = -2:1:4
x =
  -2  -1   0   1   2   3   4

[h,p,k,c] = kstest(x,[],0.05,0)
h =
   0
p =
   0.13632
k =
   0.41277
c =
   0.48342

The test fails to reject the null hypothesis that the values come from a standard normal distribution.

2、Two-sample Kolmogorov-Smirnov test

检验两个数据向量之间的分布的。

>>[h,p,ks2stat] = kstest2(x1,x2,alpha,tail)

% x1,x2都为向量，ALPHA是显著性水平（默认0.05）。TAIL是表示检验的类型（默认unequal,不平衡）。

例如，x = -1:1:5
y = randn(20,1);
[h,p,k] = kstest2(x,y)
h =
     0
p =
    0.0774
k =
    0.5214

wiki翻译起来太麻烦，还有可能曲解本意，最好看原版解释。

In statistics, the Kolmogorov–Smirnov test (K–S test) is a form of minimum distance estimation used as a nonparametric test of equality of one-dimensional probability distributions used to compare a sample with a reference probability distribution (one-sample K–S test), or to compare two samples (two-sample K–S test). The Kolmogorov–Smirnov statistic quantifies a distance between theempirical distribution function of the sample and the cumulative distribution function of the reference distribution, or between the empirical distribution functions of two samples. The null distribution of this statistic is calculated under the null hypothesis that the samples are drawn from the same distribution (in the two-sample case) or that the sample is drawn from the reference distribution (in the one-sample case). In each case, the distributions considered under the null hypothesis are continuous distributions but are otherwise unrestricted.

The two-sample KS test is one of the most useful and general nonparametric methods for comparing two samples, as it is sensitive to differences in both location and shape of the empirical cumulative distribution functions of the two samples.

The Kolmogorov–Smirnov test can be modified to serve as a goodness of fit test. In the special case of testing for normality of the distribution, samples are standardized and compared with a standard normal distribution. This is equivalent to setting the mean and variance of the reference distribution equal to the sample estimates, and it is known that using the sample to modify the null hypothesis reduces the power of a test. Correcting for this bias leads to theLilliefors test. However, even Lilliefors' modification is less powerful than the Shapiro–Wilk test or Anderson–Darling test for testing normality.^[1]