反汇编分析C语言

环境

VC6.0环境

空函数反汇编

#include "stdafx.h"
void function(){

}
int main(int argc, char* argv[])
{
	function();
	printf("Hello World!\n");
	return 0;
}

我们通过反汇编来分析这段空函数

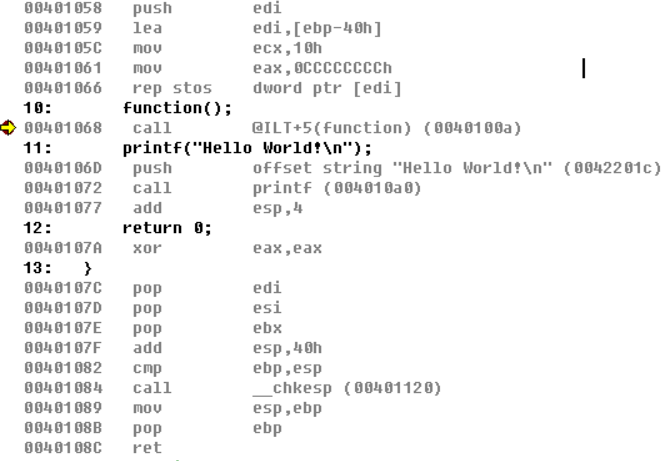
###函数外部
10:       function();
00401068   call        @ILT+5(function) (0040100a)
11:       printf("Hello World!\n");
0040106D   push        offset string "Hello World!\n" (0042201c)
00401072   call        printf (004010a0)
00401077   add         esp,4
12:       return 0;
0040107A   xor         eax,eax

函数内部

4:    #include "stdafx.h"
5:    void function(){
00401020   push        ebp
00401021   mov         ebp,esp
00401023   sub         esp,40h
00401026   push        ebx
00401027   push        esi
00401028   push        edi
00401029   lea         edi,[ebp-40h]
0040102C   mov         ecx,10h
00401031   mov         eax,0CCCCCCCCh
00401036   rep stos    dword ptr [edi]
6:
7:    }
00401038   pop         edi
00401039   pop         esi
0040103A   pop         ebx
0040103B   mov         esp,ebp
0040103D   pop         ebp
0040103E   ret

分析函数

函数调用

00401048   call        @ILT+5(function) (0040100a)

函数内部

接着进到函数的内部

有了之前画堆栈的经验，我们不难看出，尽管我们的函数是个空函数，但其汇编代码依然完成了以下流程：

1.提升堆栈

2.保护现场

3.初始化提升的堆栈

4.恢复现场

5.返回

提升堆栈

00401010   push        ebp
00401011   mov         ebp,esp
00401013   sub         esp,40h

保护现场

00401026   push        ebx
00401027   push        esi
00401028   push        edi

初始化提升的堆栈

00401029   lea         edi,[ebp-40h]
0040102C   mov         ecx,10h
00401031   mov         eax,0CCCCCCCCh
00401036   rep stos    dword ptr [edi]

恢复现场

00401028   pop         edi
00401029   pop         esi
0040102A   pop         ebx
0040102B   mov         esp,ebp
0040102D   pop         ebp

PS:这里的mov esp，ebp就是降低堆栈，与前面的提升堆栈相对应，所以也属于恢复现场的一部分

返回

0040103E   ret

函数返回后

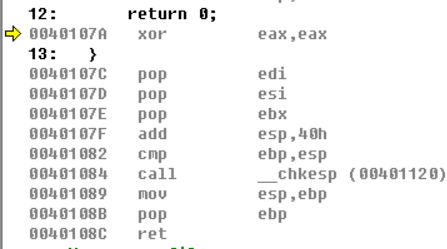
函数返回后不出意料地返回调用CALL地下一行语句，我们接着看

0040104D   xor         eax,eax

这里是将eax清零，注意到我们的语句为return 0 这里就是将eax作为返回值来传递

一般来说eax都是作为函数的返回值，但不绝对，有的函数返回值是存在内存里或其他情况，要具体情况具体分析

0040104F   pop         edi
00401050   pop         esi
00401051   pop         ebx

很明显，这里是在还原现场，别忘了我们的主程序main本身也是个函数，这是在还原main前保护的现场

接着往下走

0040107F   add         esp,40h
00401082   cmp         ebp,esp
00401084   call        __chkesp (00401120)

这里首先是将esp减少了40h，然后比较ebp和esp，最后再调用一个chesp函数从名称就不难看出 chkesp = check esp，检查esp，这个函数就是用来检查堆栈是否平衡的

那么接下来

00401089   mov         esp,ebp
0040108B   pop         ebp

依旧是恢复现场

最后是

0040108C   ret
##总结空函数分析
我们可以看到，即便是一个空函数什么都没有做，但调用一个空函数所产生的汇编代码却不少
保护现场、恢复现场以及堆栈平衡的检查等等都没少，可谓麻雀虽小五脏俱全。

简单加法函数反汇编

#include "stdafx.h"
int Plus(int x ,int y)
{
  retuen x+y;
}
int main(int argc, char* argv[])
{
	//调用加法函数
        Plus(1,2);
	return 0;
}

加法函数的反汇编

11:       //调用加法函数
12:       Plus(1,2);
00401068   push        2
0040106A   push        1
0040106C   call        @ILT+0(Plus) (00401005)
00401071   add         esp,8
13:       return 0;
00401074   xor         eax,eax
14:   }
00401076   pop         edi
00401077   pop         esi
00401078   pop         ebx
00401079   add         esp,40h
0040107C   cmp         ebp,esp
0040107E   call        __chkesp (004010a0)
00401083   mov         esp,ebp
00401085   pop         ebp
00401086   ret

分析函数

00401068   push        2
0040106A   push        1
0040106C   call        @ILT+0(Plus) (00401005)

结合前面的空函数分析，我们可以明显发现这里的函数调用环节，多了两个push就是将函数所需要的参数压入堆栈，这里的参数为2和1，注意压入的顺序是反着（由调用约定决定）

函数内部

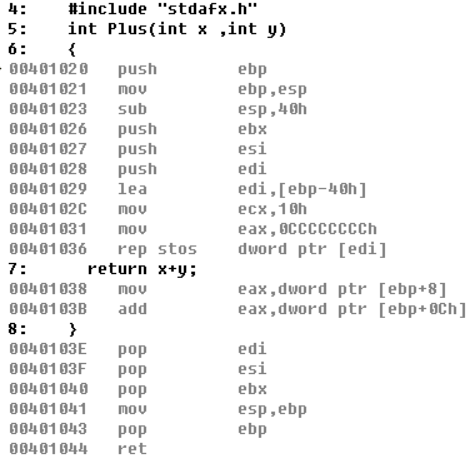
提升堆栈保护现场初始化

提升堆栈、保护现场、初始化部分和空函数如出一辙，这里就不在赘述

00401020   push        ebp
00401021   mov         ebp,esp
00401023   sub         esp,40h
00401026   push        ebx
00401027   push        esi
00401028   push        edi
00401029   lea         edi,[ebp-40h]
0040102C   mov         ecx,10h
00401031   mov         eax,0CCCCCCCCh
00401036   rep stos    dword ptr [edi]

实际执行主要的部分

7:      return x+y;
00401038   mov         eax,dword ptr [ebp+8]
0040103B   add         eax,dword ptr [ebp+0Ch]

这里的[ebp+8] 就是我们前面压入的参数1，[ebp+c]就是前面压入的参数2

于是这两条语句其实就是

00401038   mov         eax,1
0040103B   add         eax,2

将1+2的结果保存到eax中，(此时eax又作为函数返回值的载体)

恢复现场和返回

接下来的内容和空函数一样了，恢复现场和返回，也不再赘述

0040103E   pop         edi
0040103F   pop         esi
00401040   pop         ebx
00401041   mov         esp,ebp
00401043   pop         ebp
00401044   ret

函数返回后

函数返回后我们会发现与先前的空函数相比多了这一行代码

00401071   add         esp,8

这里是对应我们前面压入的两个参数1和2，压入参数后esp减少了8，这里我们函数调用结束后，就不再需要之前压入的两个参数了，于是将esp恢复到压入参数前，这其实也算是恢复现场，用来平衡堆栈，我们可以发现，这条语句是在我们call调用完毕后执行的平衡堆栈操作，所以这种操作也被称为堆栈外平衡

与之相对应的就是堆栈内平衡:即在call里面就把堆栈平衡好了