神经网络优化篇：理解指数加权平均数（Understanding exponentially weighted averages）

理解指数加权平均数

回忆一下这个计算指数加权平均数的关键方程。

\({{v}_{t}}=\beta {{v}_{t-1}}+(1-\beta ){{\theta }_{t}}\)

\(\beta=0.9\)的时候，得到的结果是红线，如果它更接近于1，比如0.98，结果就是绿线，如果\(\beta\)小一点，如果是0.5，结果就是黄线。

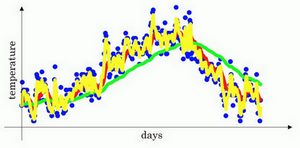
进一步地分析，来理解如何计算出每日温度的平均值。

同样的公式，\({{v}_{t}}=\beta {{v}_{t-1}}+(1-\beta ){{\theta }_{t}}\)

使\(\beta=0.9\)，写下相应的几个公式，所以在执行的时候，\(t\)从0到1到2到3，\(t\)的值在不断增加，为了更好地分析，写的时候使得\(t\)的值不断减小，然后继续往下写。

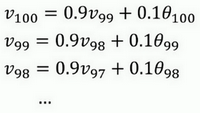
首先看第一个公式，理解\(v_{100}\)是什么？调换一下这两项（\(0.9v_{99}0.1\theta_{100}\)），\(v_{100}= 0.1\theta_{100} + 0.9v_{99}\)。

那么\(v_{99}\)是什么？就代入这个公式（\(v_{99} = 0.1\theta_{99} +0.9v_{98}\)），所以：

\(v_{100} = 0.1\theta_{100} + 0.9(0.1\theta_{99} + 0.9v_{98})\)。

那么\(v_{98}\)是什么？可以用这个公式计算（\(v_{98} = 0.1\theta_{98} +0.9v_{97}\)），把公式代进去，所以：

\(v_{100} = 0.1\theta_{100} + 0.9(0.1\theta_{99} + 0.9(0.1\theta_{98} +0.9v_{97}))\)。

以此类推，如果把这些括号都展开，

\(v_{100} = 0.1\theta_{100} + 0.1 \times 0.9 \theta_{99} + 0.1 \times {(0.9)}^{2}\theta_{98} + 0.1 \times {(0.9)}^{3}\theta_{97} + 0.1 \times {(0.9)}^{4}\theta_{96} + \ldots\)

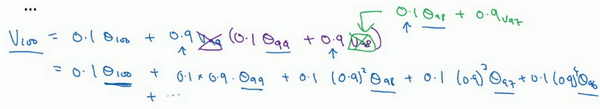
所以这是一个加和并平均，100号数据，也就是当日温度。分析\(v_{100}\)的组成，也就是在一年第100天计算的数据，但是这个是总和，包括100号数据，99号数据，97号数据等等。画图的一个办法是，假设有一些日期的温度，所以这是数据，这是\(t\)，所以100号数据有个数值，99号数据有个数值，98号数据等等，\(t\)为100，99，98等等，这就是数日的温度数值。

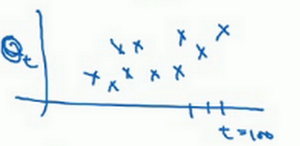
然后构建一个指数衰减函数，从0.1开始，到\(0.1 \times 0.9\)，到\(0.1 \times {(0.9)}^{2}\)，以此类推，所以就有了这个指数衰减函数。

计算\(v_{100}\)是通过，把两个函数对应的元素，然后求和，用这个数值100号数据值乘以0.1，99号数据值乘以0.1乘以\({(0.9)}^{2}\)，这是第二项，以此类推，所以选取的是每日温度，将其与指数衰减函数相乘，然后求和，就得到了\(v_{100}\)。

结果是，稍后详细讲解，不过所有的这些系数（\(0.10.1 \times 0.90.1 \times {(0.9)}^{2}0.1 \times {(0.9)}^{3}\ldots\)），相加起来为1或者逼近1，称之为偏差修正。

最后也许会问，到底需要平均多少天的温度。实际上\({(0.9)}^{10}\)大约为0.35，这大约是\(\frac{1}{e}\)，e是自然算法的基础之一。大体上说，如果有\(1-\varepsilon\)，在这个例子中，\(\varepsilon=0.1\)，所以\(1-\varepsilon=0.9\)，\({(1-\varepsilon)}^{(\frac{1}{\varepsilon})}\)约等于\(\frac{1}{e}\)，大约是0.34，0.35，换句话说，10天后，曲线的高度下降到\(\frac{1}{3}\)，相当于在峰值的\(\frac{1}{e}\)。

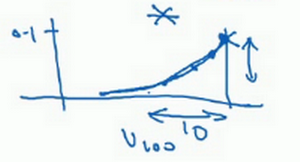
又因此当\(\beta=0.9\)的时候，说仿佛在计算一个指数加权平均数，只关注了过去10天的温度，因为10天后，权重下降到不到当日权重的三分之一。

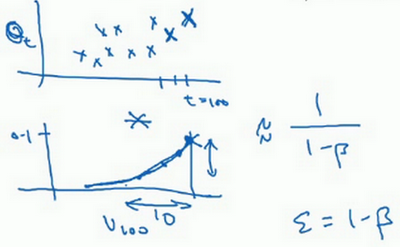
相反，如果，那么0.98需要多少次方才能达到这么小的数值？\({(0.98)}^{50}\)大约等于\(\frac{1}{e}\)，所以前50天这个数值比\(\frac{1}{e}\)大，数值会快速衰减，所以本质上这是一个下降幅度很大的函数，可以看作平均了50天的温度。因为在例子中，要代入等式的左边，\(\varepsilon=0.02\)，所以\(\frac{1}{\varepsilon}\)为50，由此得到公式，平均了大约\(\frac{1}{(1-\beta)}\)天的温度，这里\(\varepsilon\)代替了\(1-\beta\)，也就是说根据一些常数，能大概知道能够平均多少日的温度，不过这只是思考的大致方向，并不是正式的数学证明。

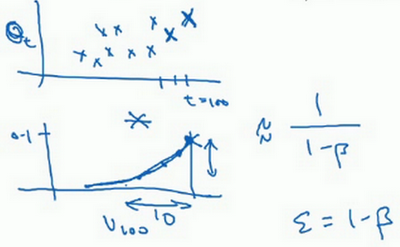
最后讲讲如何在实际中执行，还记得吗？一开始将\(v_{0}\)设置为0，然后计算第一天\(v_{1}\)，然后\(v_{2}\)，以此类推。

现在解释一下算法，可以将\(v_{0}\)，\(v_{1}\)，\(v_{2}\)等等写成明确的变量，不过在实际中执行的话，要做的是，一开始将\(v\)初始化为0，然后在第一天使\(v:= \beta v + (1 - \beta)\theta_{1}\)，然后第二天，更新\(v\)值，\(v: = \beta v + (1 -\beta)\theta_{2}\)，以此类推，有些人会把\(v\)加下标，来表示\(v\)是用来计算数据的指数加权平均数。

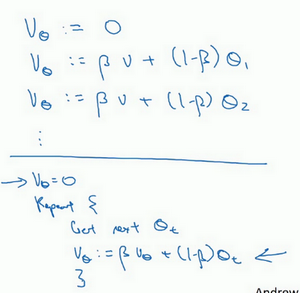
再说一次，但是换个说法，\(v_{\theta} =0\)，然后每一天，拿到第\(t\)天的数据，把\(v\)更新为\(v: = \beta v_{\theta} + (1 -\beta)\theta_{t}\)。

指数加权平均数公式的好处之一在于，它占用极少内存，电脑内存中只占用一行数字而已，然后把最新数据代入公式，不断覆盖就可以了，正因为这个原因，其效率，它基本上只占用一行代码，计算指数加权平均数也只占用单行数字的存储和内存，当然它并不是最好的，也不是最精准的计算平均数的方法。如果要计算移动窗，直接算出过去10天的总和，过去50天的总和，除以10和50就好，如此往往会得到更好的估测。但缺点是，如果保存所有最近的温度数据，和过去10天的总和，必须占用更多的内存，执行更加复杂，计算成本也更加高昂。