HOW MANY OF THEM?(让人匪夷所思的一题)

题面

由n个节点构成的，割边数不超过m条的无向连通图个数(无自环和重边），答案对1e9+7取模。

\[-------------------------------------------
\]

真是越简单的题目越难（其实越难的题目也越难）

这篇题解主要是再将rainbow的思路理一遍：

\[-------------------------------------------
\]

毫无疑问，首先定义一个f[i][j]表示由i个点构成j条割边的方案数，那么该怎么转移呢？

注意到题目中有割边这个限制，割边是什么？

割边就是去掉这条边之后会将一个连通块分裂成两个以上的连通块的边

那么我们就可以以1号点为基准，枚举将1号点所在双连通分量去掉后，整张图将会分裂成什么样子

首先枚举1号点所在双连通分量大小为k，还需要从其他i-1个点中选出k-1个点来组成这个双连通分量，有$$\sum_{k=1}^{i-1} {f[k][0]*C_{i-1}^{k-1}}$$种情况,接下来枚举剩下的图的情况，g[i][j][k]表示由i个点构成了j个连通块其中有k条割边的情况数，枚举去掉一号双连通分量后图分裂为了几个连通块，如图：



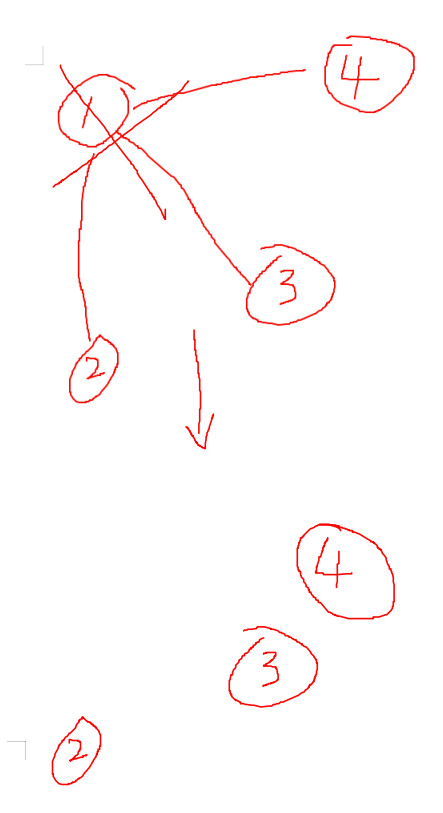
设x是分裂后还剩的连通块数量，那么每个连通块都和原来的1号双连通分量连着一条割边，也就还剩下j-x条割边，有$$\large\sum_{x=1}^{\min(i-k,j)} g[i-k][x][j-x]$$种图，他们还需要与原来的1号双连通分量相连，在每个连通块内任选一个点与1号双连通分量中任意一个点相连,但是每个连通块的大小我们不方便在这里枚举，\(\huge{所以先搁置不管，一会求g[i][j][k]时再算}\)，因与一号双联相连，乘上\(k^x\).

那么我们可以得到f[i][j]的转移方程：$$f[i][j]= \sum_{k=1}^{i-1} (f[k][0] * C_{i-1}^{k-1} * \sum_{x=1}^{\min(i-k,j)} g[i-k][x][j-x] * k^x)$$

但是这仅对j>0的情况有用，那么f[i][0]怎么求呢？ 那么我们在做这道题之前应该已经做过一道求n个节点的无向连通图的个数的题（Connected Graph）了，在这里再引用一下：

设\(h[i]\)表示有i个节点的连通图个数，只需要用所有情况-不联通的情况即可。那么所有的情况就是任意两点之间连不连边都可以，就有\(\large2^{i*(i-1)/2}\)，我们枚举1号点所在连通图的大小k，还需要在i-1个节点中再选出k-1个节点来构成一号连通图，有$$\large h[k]*C_{i-1}^{k-1}$$种情况，剩下的i-k个点随便构成怎样的都行,就有\(\large2^{(i-k)*(i-k-1)/2}\)种情况。

那么可以得到h[i]的转移方程:

\[\large h[i]=2^{i(i-1)/2} - \sum_{j=1}^{i-1} h[j] * C_{i-1}^{j-1} * 2^{(i-j)(i-j-1)/2}
\]

那么f[i][0]也可求得：

\[\large f[i][0]= h[i] - \sum_{j=1}^{i-1} f[i][j]
\]

就下来就只剩g[i][j][k]没有解决了，我们\(\huge照葫芦画瓢\),也去找一个基准，也就是1号点所在连通块，将其去掉后，就可以将g[i][j][k]由已知状态转移过来，需要枚举f[l1][l2].还有不要忘记我们刚才求f[i][j]时有一个连边所用的点没有算，还需要乘上一号连通块大小l1.

可得g[i][j][k]的状态转移方程:

\[\large g[i][j][k]= \sum_{l_1=1}^{i} \sum_{l_2=0}^{k} f[l_1][l_2] * C_{i-1}^{l_{1}-1} * l_1 * g[i-l_1][j-1][k-l_2]
\]

到这里，我们已经推出了所有的转移方程

$$\large f[i][j]= \sum_{k=1}^{i-1} (f[k][0] * C_{i-1}^{k-1} * \sum_{x=1}^{\min(i-k,j)} g[i-k][x][j-x] * k^x)$$

$$\large h[i]=2^{i(i-1)/2} - \sum_{j=1}^{i-1} h[j] * C_{i-1}^{j-1} * 2^{(i-j)(i-j-1)/2}$$

$$\large f[i][0]= h[i] - \sum_{j=1}^{i-1} f[i][j]$$

$$\large g[i][j][k]= \sum_{l_1=1}^{i} \sum_{l_2=0}^{k} f[l_1][l_2] * C_{i-1}^{l_{1}-1} * l_1 * g[i-l_1][j-1][k-l_2] $$

只需要有上面的转移方程一步一步来就可以切了这道狗屎题。

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef long double ld;
#define ps push_back
#define mk make_pair
#define fi first
#define se second
const int N=55,inf=0x7f7f7f7f;
const ll linf=0x3f7f7f7f7f7f7f7f,mod=1e9+7;
inline ll read(){
	char c=getchar();ll x=0,f=1;
	while(c<'0'||c>'9')f=c=='-'?-1:1,c=getchar();
	while(c>='0'&&c<='9')x=(x<<1)+(x<<3)+(c^48),c=getchar();
	return x*f;
}
ll n,m,f[N][N],g[N][N][N],h[N],c[N][N],ci2[N*N];
inline ll qp(ll x,int y){
	ll ans=1;
	while(y){
		if(y&1)ans=ans*x%mod;
		x=x*x%mod;y>>=1;
	}
	return ans;
}
int main(){
	#ifndef ONLINE_JUDGE
	freopen("in.in","r",stdin);
	freopen("out.out","w",stdout);
	#endif
	n=read();
	m=min(n,read());
	ci2[0]=1;
	for(int i=1;i<=2500;++i)
		ci2[i]=(ci2[i-1]<<1)%mod;
	c[0][0]=1;
	for(int i=1;i<=50;++i){
		c[i][0]=1;
		for(int j=1;j<=i;++j)
			c[i][j]=(c[i-1][j]+c[i-1][j-1])%mod;
	}
	// h[1]=1;
	for(int i=1;i<=n;++i){//h suan
		h[i]=ci2[i*(i-1)>>1];
		for(int j=1;j<i;++j){
			h[i]=(h[i]-h[j]*c[i-1][j-1]%mod*ci2[(i-j)*(i-j-1)>>1]%mod+mod)%mod;
		}
	}
	g[0][0][0]=1;
	for(int i=1;i<=n;++i){
		for(int j=1;j<i;++j){
			for(int k=1;k<i;++k){
				ll op=0;
				for(int x=1;x<=min(i-k,j);++x){
					op=(op+g[i-k][x][j-x]*qp(k,x)%mod)%mod;
				}
				f[i][j]=(f[i][j]+f[k][0]*op%mod*c[i-1][k-1]%mod)%mod;
			}
		}
		f[i][0]=h[i];
		for(int j=1;j<i;++j)
			f[i][0]-=f[i][j];
		f[i][0]=(f[i][0]%mod+mod)%mod;
		for(int j=1;j<=i;++j){
			for(int k=0;k<i;++k){
				for(int l1=1;l1<=i;++l1){
					ll op=0;
					for(int l2=0;l2<=k;++l2){
						op=(op+f[l1][l2]*g[i-l1][j-1][k-l2]%mod)%mod;
					}
					g[i][j][k]+=op*c[i-1][l1-1]%mod*l1%mod;
				}
				g[i][j][k]%=mod;
			}
		}
	}
	ll ans=0;
	for(int i=0;i<=m;++i)
		ans+=f[n][i];
	printf("%lld\n",ans%mod);
}

\[\huge pu-tao↑zher↑↓
\]