「P3385」【模板】负环（spfa

题目描述

暴力枚举/SPFA/Bellman-ford/奇怪的贪心/超神搜索

输入输出格式

输入格式：

第一行一个正整数T表示数据组数，对于每组数据：

第一行两个正整数N M，表示图有N个顶点，M条边

接下来M行，每行三个整数a b w，表示a->b有一条权值为w的边（若w<0则为单向，否则双向）

输出格式：

共T行。对于每组数据，存在负环则输出一行"YE5"(不含引号)，否则输出一行"N0"(不含引号)。

输入输出样例

输入样例#1：复制

输出样例#1：复制

N0

YE5

说明

n\leq 2000n≤2000m\leq 3000m≤3000-10000\leq w\leq 10000−10000≤w≤10000T\leq 10T≤10建议复制输出格式中的字符串。本题数据感谢@negiizhao的精心构造，请不要使用玄学算法本题数据有更新

题解

枚举每个点，如果该点未被遍历过，则以其为起点跑spfa。（防止图不连通

跑的过程中记一下每个点被经历的次数，如果被经历（学术说法松弛？）了超过n次，说明这里出现了负环。

算是spfa的一个小技巧？

————————————

然后是年度悲情大戏之——我的STLqueue不可能这么慢↓

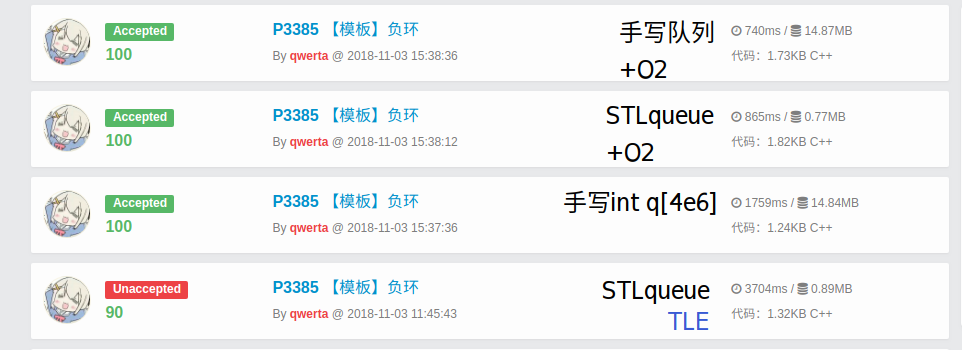
我的妈我这么爱用的STLqueue这么慢？！！

老姐你把我的时间直接拖长了一倍不止啊？！！（气哭

还以为自己哪里写的太丑了......

 /*

 qwerta

 P3385 【模板】负环 Accepted

 100

 代码 C++，1.24KB

 提交时间 2018-11-03 15:37:36

 耗时/内存 1759ms, 15192KB

 */

 #include<iostream>

 #include<cstring>

 #include<cstdio>

 #include<queue>

 using namespace std;

 struct emm{

     int e,f,l;

 }a[];

 int h[];

 int tot;

 void con(int x,int y,int l)

 {

     //cout<<"con "<<x<<" "<<y<<" "<<l<<endl;

     a[++tot].f=h[x];

     h[x]=tot;

     a[tot].e=y;

     a[tot].l=l;

     return;

 }

 const int INF=1e9+;

 int d[];

 int c[];

 bool sf[];

 bool vis[];

 int q[];//时间减半的手写队列

 int main()

 {

     //freopen("a.in","r",stdin);

     int t;

     scanf("%d",&t);

     while(t--)

     {

         tot=;

         memset(h,,sizeof(h));

         int n,m;

         scanf("%d%d",&n,&m);

         for(int i=;i<=m;++i)

         {

             int x,y,l;

             scanf("%d%d%d",&x,&y,&l);

             if(l<)

             con(x,y,l);

             else

             con(x,y,l),con(y,x,l);

         }

         int flag=;

         memset(d,,sizeof(d));

         memset(c,,sizeof(c));

         memset(vis,,sizeof(vis));

         for(int s=n;s>=&&!flag;--s)

         if(!vis[s])

         {

             memset(sf,,sizeof(sf));

             d[s]=;sf[s]=;q[]=s;

             int l=,r=;

             while(l<r&&!flag)

             {

                 int x=q[++l];

                 vis[x]=;

                 for(int i=h[x];i;i=a[i].f)

                 if(d[a[i].e]>d[x]+a[i].l)

                 {

                     d[a[i].e]=d[x]+a[i].l;

                     c[a[i].e]++;

                     if(c[a[i].e]>=n){flag++;break;}

                     if(!sf[a[i].e])

                     {

                         sf[a[i].e]=;

                         q[++r]=a[i].e;

                     }

                 }

                 sf[x]=;

             }

             d[s]=INF;

         }

         if(flag)cout<<"YE5"<<endl;

         else cout<<"N0"<<endl;

     }

     return ;

 }