Applied Nonparametric Statistics-lec1

参考网址：

https://onlinecourses.science.psu.edu/stat464/node/2

---

• Binomial Distribution

• Normal Distribution

将正态分布标准化。这也就是Z-score

• Confidence Interval

在上面的前提下，假设σ^2已知，现在构造μ的置信区间：

利用上面Z-score的公式，且

套入公式，解出μ。注意此处的标准差用的是σ/根号n。最终解出：

当σ^2=Var(X)不知道时，我们可以用样本的标准差，计算Z-score，这样的话，是服从一个自由度为n-1的t分布。

同样的计算过程，可得μ的置信区间为：

• Hypothesis Tests

同样是在上面的前提下，已知σ^2，我们对μ做一个假设，比如看它与另一个值μ0相比，大小如何？我们可以有以下几个假设：

要考虑找出p值，帮助我们判断是否要拒绝原假设。我们使用统计量

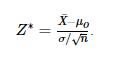
计算出p值。如果它小于给定的显著性水平α，就拒绝原假设，否则要接受。

同样的，当σ^2未知时，我们用样本的标准差代替，此时也需要使用自由度为n-1的t分布。同样计算。