POJ 1419 Graph Coloring（最大独立集/补图的最大团）

Graph Coloring

Time Limit: 1000MS		Memory Limit: 10000K
Total Submissions: 4893		Accepted: 2271		Special Judge

Description

You are to write a program that tries to find an optimal coloring for a given graph. Colors are applied to the nodes of the graph and the only available colors are black and white. The coloring of the graph is called optimal if a maximum of nodes is black. The coloring is restricted by the rule that no two connected nodes may be black.

 
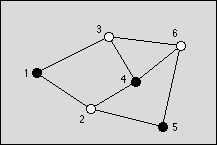
Figure 1: An optimal graph with three black nodes 

Input

The graph is given as a set of nodes denoted by numbers 1...n, n <= 100, and a set of undirected edges denoted by pairs of node numbers (n1, n2), n1 != n2. The input file contains m graphs. The number m is given on the first line. The first line of each graph
contains n and k, the number of nodes and the number of edges, respectively. The following k lines contain the edges given by a pair of node numbers, which are separated by a space.

Output

The output should consists of 2m lines, two lines for each graph found in the input file. The first line of should contain the maximum number of nodes that can be colored black in the graph. The second line should contain one possible optimal coloring. It is
given by the list of black nodes, separated by a blank.

Sample Input

1
6 8
1 2
1 3
2 4
2 5
3 4
3 6
4 6
5 6

Sample Output

3
1 4 5

Source

Southwestern European Regional Contest 1995

题目链接：POJ 1419

模版题，熟悉一下写法和过程

代码：

#include<iostream>
#include<algorithm>
#include<cstdlib>
#include<sstream>
#include<cstring>
#include<cstdio>
#include<string>
#include<deque>
#include<stack>
#include<cmath>
#include<queue>
#include<set>
#include<map>
using namespace std;
#define INF 0x3f3f3f3f
#define CLR(x,y) memset(x,y,sizeof(x))
#define LC(x) (x<<1)
#define RC(x) ((x<<1)+1)
#define MID(x,y) ((x+y)>>1)
typedef pair<int,int> pii;
typedef long long LL;
const double PI=acos(-1.0);

const int N=110;

bool E[N][N];
int x[N],opt[N];
int n,m,ans,cnt,maxn,vis[N<<2];

void dfs(int i)
{
	int j;
	if(i>n)
	{
		ans=cnt;
		for (j=1; j<=n; ++j)
			opt[j]=x[j];
	}
	else
	{
		bool flag=true;
		for (j=1; j<i&&flag; ++j)
		{
			if(x[j]==1&&!E[j][i])
				flag=false;
		}
		if(flag)
		{
			x[i]=1;
			++cnt;
			dfs(i+1);
			--cnt;
		}
		if(cnt+n-i>ans)
		{
			x[i]=0;
			dfs(i+1);
		}
	}
}
void init()
{
	CLR(E,true);
	CLR(x,0);
	CLR(opt,0);
	maxn=ans=cnt=0;
	CLR(vis,0);
}
int main(void)
{
	int i,j,tcase,x,y;
	scanf("%d",&tcase);
	while (~scanf("%d%d",&n,&m))
	{
		init();
		scanf("%d%d",&n,&m);
		for (i=0; i<m; ++i)
		{
			scanf("%d%d",&x,&y);
			E[x][y]=E[y][x]=false;
		}
		dfs(1);
		printf("%d\n",ans);
		for (i=1; i<n; ++i)
			if(opt[i])
				printf("%d ",i);
		putchar('\n');
	}
	return 0;
}